Trayectoria hiperbólica para niños
Una trayectoria hiperbólica es el camino que sigue un objeto en el espacio cuando su velocidad es tan alta que puede escapar de la atracción de la gravedad de un cuerpo central, como un planeta o una estrella. Imagina que lanzas una pelota hacia arriba con tanta fuerza que nunca vuelve a caer. Eso sería una trayectoria de escape.
Según las leyes de la física de Isaac Newton, este tipo de camino tiene la forma de una hipérbola. Esto significa que el objeto se acerca al cuerpo central, lo rodea y luego se aleja para siempre, sin volver. En términos más técnicos, decimos que la excentricidad orbital de esta trayectoria es mayor que uno.
Un objeto que sigue una trayectoria hiperbólica se dirige hacia el infinito, manteniendo una velocidad extra incluso cuando está muy lejos del cuerpo central. Al igual que las trayectorias parabólicas, las hiperbólicas son caminos de escape. La energía que tiene un objeto en una trayectoria hiperbólica siempre es positiva.
Las naves espaciales a menudo usan trayectorias hiperbólicas cuando realizan una asistencia gravitatoria (también conocida como "tirón gravitatorio") para acelerar o cambiar de dirección al pasar cerca de un planeta.
Contenido
¿Qué define una trayectoria hiperbólica?
Para entender una trayectoria hiperbólica, usamos varios números y medidas. Algunos de estos son similares a los que se usan para describir las órbitas elípticas (como las de los planetas alrededor del Sol), pero otros son específicos de las trayectorias de escape.
Semieje mayor, energía y velocidad de escape
El semieje mayor (representado con la letra a) es un concepto un poco diferente en una trayectoria hiperbólica. Aunque no es una distancia física que se pueda ver fácilmente, se usa en las fórmulas. Por lo general, se le da un valor negativo para que las ecuaciones funcionen bien con las de las órbitas elípticas.
Este semieje mayor está directamente relacionado con la energía orbital específica y con la velocidad hiperbólica excedente (representada como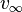 
). Esta última es la velocidad que el objeto tendría si estuviera infinitamente lejos del cuerpo central.
- La fórmula que los relaciona es:*
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): v_{\infty}^2 = -\mu/a Donde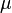 
es el parámetro gravitacional estándar (que depende de la masa del cuerpo central).
Es importante recordar que la energía total de un objeto en una trayectoria hiperbólica es positiva. En cambio, para una órbita elíptica, la energía es negativa.
Excentricidad y ángulo de las asíntotas
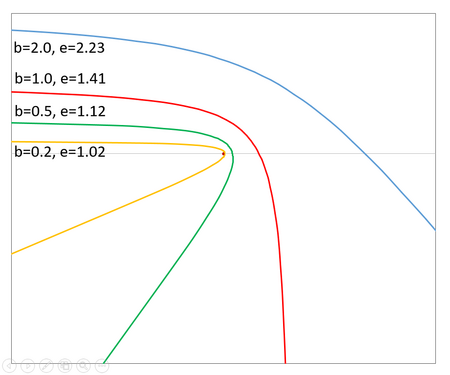
La excentricidad orbital (representada con la letra e) de una trayectoria hiperbólica siempre es mayor que 1. Este valor nos dice qué tan "abierta" es la forma de la hipérbola.
- Si la excentricidad es apenas mayor que 1, la hipérbola es muy cerrada, como una "V" aguda.
- Si la excentricidad es
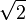(aproximadamente 1.414), las líneas de la hipérbola (llamadas asíntotas) forman un ángulo recto. - A medida que la excentricidad aumenta, la trayectoria se vuelve más y más parecida a una línea recta.
El ángulo entre la dirección de máxima aproximación al cuerpo central (periapsis) y una de las asíntotas se llama anomalía verdadera en el infinito (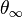
). El ángulo total entre la dirección de llegada y la de salida del objeto es el doble de este valor (Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 2\theta_\infty ).
- La relación es:*
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \theta{_\infty}=\cos^{-1}(1/e)
Parámetro de impacto y distancia más cercana
El parámetro de impacto (representado con la letra b) es la distancia a la que un objeto pasaría del cuerpo central si no fuera afectado por su gravedad. En las trayectorias hiperbólicas, este parámetro es igual al semieje menor de la hipérbola.
Cuando una nave espacial o un cometa se acercan a un planeta, conocemos su parámetro de impacto y su velocidad. Con esta información, podemos calcular la distancia mínima a la que se acercará al planeta (la distancia del periapsis,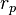 
). Si esta distancia es menor que el radio del planeta, ¡habrá una colisión!
- La fórmula para la distancia del periapsis es:*
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): r_p = a(e-1)
Por ejemplo, si un cometa se acerca a la Tierra con una velocidad de 12.5 km/s, para evitar chocar, su parámetro de impacto debe ser de al menos 8600 km. Esto es un 34% más grande que el radio de la Tierra.
Si no conocemos la masa del cuerpo central, podemos calcularla observando cuánto se desvía el objeto que pasa cerca, junto con su parámetro de impacto y su velocidad de aproximación. Esto es muy útil para las misiones espaciales que sobrevuelan planetas, ya que les permite medir con precisión la masa de esos cuerpos.
Ecuaciones del movimiento
Las ecuaciones nos ayudan a describir exactamente dónde estará un objeto en una trayectoria hiperbólica en un momento dado y a qué velocidad.
Posición
La posición de un objeto en una trayectoria hiperbólica se puede describir usando la anomalía verdadera (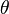
), que es el ángulo entre el punto más cercano al cuerpo central y la posición actual del objeto.
- La ecuación que relaciona la distancia (
) con la anomalía verdadera es:*
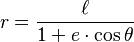Donde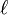 
es el semiancho recto.
También usamos la anomalía excéntrica (E) y la anomalía media (M) para calcular la posición en el tiempo. La anomalía media está directamente relacionada con el tiempo que ha pasado desde el punto más cercano.
Ángulo de la trayectoria de vuelo
El ángulo de la trayectoria de vuelo (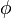
) es el ángulo entre la dirección en la que se mueve el objeto y una línea perpendicular a la que lo une con el cuerpo central. Este ángulo es cero cuando el objeto está en su punto más cercano y se acerca a 90 grados cuando está muy lejos.
- La fórmula es:*
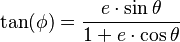
Velocidad
La velocidad de un objeto en una trayectoria hiperbólica se puede calcular con la ecuación vis-viva:
*
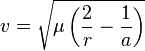Donde:
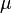es el parámetro gravitacional estándar.
es la distancia del objeto al cuerpo central.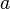
es el semieje mayor (que es negativo).
Una relación importante es que la velocidad al cuadrado de un objeto (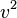
) es igual a la velocidad de escape local al cuadrado (Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): {v_{esc}}^2 ) más la velocidad hiperbólica excedente al cuadrado (Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): v_\infty^2 ):
*
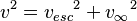Esto significa que un pequeño aumento en la velocidad cuando un objeto ya está cerca de la velocidad de escape puede resultar en una velocidad mucho mayor cuando el objeto está muy lejos. Esto se conoce como el Efecto Oberth. Lo contrario también es cierto: un objeto no necesita reducir mucho su velocidad para ser capturado por la gravedad de un planeta.
Trayectoria hiperbólica radial
Una trayectoria hiperbólica radial es un caso especial donde el objeto se mueve en línea recta, directamente hacia o desde el cuerpo central. En este caso, la velocidad del objeto siempre es mayor que la velocidad de escape. Es como una órbita hiperbólica donde el semieje menor es cero y la excentricidad es 1, pero no es una órbita parabólica.
Trayectorias en la relatividad general
En la relatividad general, que es una teoría más avanzada de la gravedad, las trayectorias de los objetos que escapan de la gravedad de otro cuerpo no tienen exactamente la forma de una hipérbola perfecta. Sin embargo, seguimos usando el término "trayectoria hiperbólica" para describir estos caminos.
Ver también
- Órbita
- Órbita de Kepler
- Sobrevuelo planetario
Véase también
En inglés: Hyperbola Facts for Kids
