Trabajo (física) para niños
Datos para niños Trabajo (W o T se pone W en inglés (work) |
||
|---|---|---|
 trabajo realizado por una fuerza constante.
|
||
| Magnitud | Trabajo (W o T se pone W en inglés (work) | |
| Definición | producto de la fuerza ejercida sobre un cuerpo por su desplazamiento | |
| Tipo | Magnitud escalar | |
| Unidad SI | julio (J) | |
| Otras unidades | kilojulio (kJ) kilográmetro (kgm) |
|
En física, el trabajo es lo que ocurre cuando una fuerza mueve un objeto. Imagina que empujas una caja: si la caja se mueve, ¡estás haciendo trabajo!
El trabajo es una forma de transferir energía. Si un objeto tiene energía, significa que puede realizar trabajo. Por ejemplo, la gasolina tiene energía que puede hacer que un coche se mueva. La energía nunca se pierde, solo se transforma.
Contenido
Trabajo en Física
El trabajo en física es un concepto clave para entender cómo las fuerzas causan movimiento. No es lo mismo que el trabajo que haces en la escuela o en casa. Aquí, se refiere a la acción de una fuerza que provoca un desplazamiento.
¿Cómo se calcula el trabajo?
Para calcular el trabajo, necesitamos saber la fuerza que se aplica y cuánto se mueve el objeto. También importa la dirección en la que se aplica la fuerza.
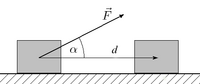
Si empujas una caja con una fuerza constante y la caja se mueve en la misma dirección en la que empujas, el trabajo se calcula multiplicando la fuerza por la distancia que se movió el objeto.
- Fuerza constante sobre un objeto:
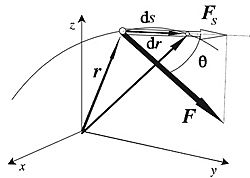
Si una fuerza empuja un objeto en línea recta, el trabajo (W) se calcula así: W = Fuerza (F) × Distancia (d) × cos(ángulo)
El "cos(ángulo)" es importante porque la fuerza debe ir en la misma dirección que el movimiento. * Si empujas y el objeto se mueve en la misma dirección, el ángulo es 0 y cos(0) es 1. * Si empujas hacia un lado y el objeto se mueve hacia adelante, el ángulo es diferente. * Si la fuerza es completamente de lado (perpendicular) al movimiento, no se realiza trabajo. Por ejemplo, si llevas una mochila en la espalda y caminas en línea recta, la fuerza de la mochila es hacia abajo, pero tú te mueves hacia adelante. En este caso, la mochila no realiza trabajo sobre ti en la dirección de tu movimiento.
Si no hay movimiento, no hay trabajo. Por ejemplo, si empujas una pared muy fuerte pero no se mueve, no estás haciendo trabajo en el sentido físico.
Trabajo y la energía de movimiento
El trabajo está muy relacionado con la energía cinética, que es la energía que tienen los objetos debido a su movimiento.
Cuando se realiza trabajo sobre un objeto, su energía cinética cambia. Si empujas un carrito y este acelera, estás haciendo trabajo sobre él y su energía de movimiento (energía cinética) aumenta.
Trabajo en sistemas elásticos
Algunos objetos, como los muelles, pueden almacenar energía cuando se estiran o se comprimen.
Estirar o comprimir un muelle
Cuando estiras o comprimes un muelle, estás realizando trabajo sobre él. El muelle, a su vez, ejerce una fuerza que intenta volver a su posición original. Esta fuerza es mayor cuanto más estires o comprimas el muelle.
El trabajo que haces para estirar o comprimir un muelle se guarda en él como energía potencial elástica. Es como cargar una batería: la energía se almacena y puede ser liberada después.
Trabajo en la termodinámica
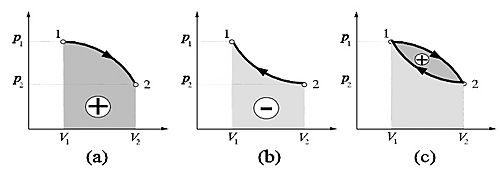
El trabajo no solo se refiere a mover objetos. En la termodinámica, que estudia el calor y la energía, el trabajo puede estar relacionado con cambios de volumen en gases o líquidos.
Por ejemplo, cuando un gas se expande dentro de un recipiente, puede realizar trabajo sobre las paredes del recipiente. Esto es importante en motores y máquinas que usan calor para generar movimiento.
Unidades de trabajo
El trabajo, al ser una forma de energía, se mide en las mismas unidades que la energía.
Sistema Internacional de Unidades (SI)
- Julio (J): Es la unidad principal de trabajo y energía en el Sistema Internacional. Un julio es el trabajo que se realiza cuando una fuerza de un newton mueve un objeto un metro. Lleva el nombre de James Prescott Joule, un físico inglés.
Otras unidades comunes
- Kilojulio (kJ): Son 1000 julios.
- Kilográmetro (kgm): Es una unidad más antigua. Un kilográmetro equivale a 9,81 julios.
- Ergio (erg): Es una unidad más pequeña. Un ergio es 0,0000001 julios (10-7 J).
- Kilovatio-hora (kW·h): Esta unidad se usa mucho para medir el consumo de electricidad en casa.
Historia del concepto de trabajo
Los antiguos griegos estudiaban cómo las máquinas simples (como palancas o poleas) podían equilibrar fuerzas. Sin embargo, no tenían el concepto de trabajo como lo conocemos hoy.
Durante el Renacimiento, los científicos comenzaron a entender que estas máquinas no solo aplicaban fuerza, sino que también movían cargas a cierta distancia. Esto llevó a la idea de que las máquinas no crean energía, sino que la transforman.
Galileo Galilei, un famoso científico italiano, fue uno de los primeros en explicar esto en el año 1600. Él mostró que las máquinas simples son como "amplificadores de fuerza" que nos ayudan a hacer trabajo de manera más eficiente.
Véase también
 En inglés: Work (physics) Facts for Kids
En inglés: Work (physics) Facts for Kids