Teorema del valor intermedio para niños
En el mundo de las matemáticas, el Teorema de los Valores Intermedios (también conocido como TVI) es una idea muy útil sobre las funciones que son continuas. Una función continua es como una línea que puedes dibujar sin levantar el lápiz del papel.
Imagina que tienes una función que empieza en un punto y termina en otro. Si la función es continua (es decir, no tiene saltos ni agujeros), este teorema nos dice que la función debe pasar por todos los valores que están entre el punto de inicio y el punto final.
Contenido
¿Qué dice el Teorema de los Valores Intermedios?
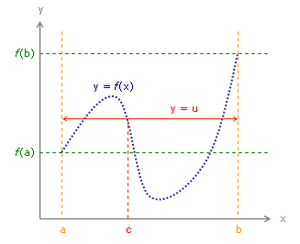
Imagina que tienes una función llamada f que es continua en un intervalo cerrado, por ejemplo, desde un número a hasta un número b. Esto significa que la función no tiene interrupciones entre a y b.
Si la función toma un valor f(a) al principio y un valor f(b) al final, entonces para cualquier número u que esté entre f(a) y f(b), ¡siempre habrá un punto c entre a y b donde la función f toma ese valor u! En otras palabras, la función "visita" todos los valores intermedios.
Ideas importantes que se derivan del TVI
- Una de las consecuencias de este teorema es que si aplicas una función continua a un intervalo, el resultado siempre será otro intervalo. Esto significa que no se "rompen" los conjuntos de números.
- El Teorema de Bolzano es un caso especial del Teorema de los Valores Intermedios.
¿Cómo se demuestra este teorema?
El Teorema de los Valores Intermedios es un "teorema de existencia". Esto significa que nos asegura que algo existe, en este caso, un número c donde la función toma un valor específico. No nos dice cuál es ese número, solo que está ahí.
Hay varias maneras de demostrarlo. Una forma común usa la idea del supremo, que es como encontrar el número más pequeño que es más grande que todos los números de un grupo.
El Teorema de Bolzano: Un caso especial
A veces, en los cursos de matemáticas, se enseña primero el Teorema de Bolzano y luego se usa para explicar el Teorema de los Valores Intermedios.
¿Qué dice el Teorema de Bolzano?
Si tienes una función f que es continua en un intervalo de a a b, y si el valor de la función al principio (f(a)) es negativo y al final (f(b)) es positivo (o viceversa), entonces debe haber al menos un punto c entre a y b donde la función es exactamente cero (f(c) = 0). Es como cruzar el nivel del mar: si empiezas bajo el agua y terminas sobre ella, en algún momento tuviste que estar justo en el nivel del mar.
Este teorema solo nos dice que existe al menos un punto donde la función es cero, no cuántos puntos son.
Demostración usando la topología
También se puede demostrar este teorema usando conceptos de la topología, una rama de las matemáticas que estudia las propiedades de los espacios. Los intervalos son "conexos" (están unidos) y las funciones continuas mantienen esa conexión. Si el punto de partida es un intervalo, la imagen (el resultado) de una función continua también será un intervalo, lo que demuestra el teorema.
Ejemplos de aplicación del TVI
- ¿Cuándo dos funciones se encuentran?
Imagina que tienes dos funciones continuas, f y g, en el mismo intervalo. Si al principio del intervalo, la diferencia entre ellas (g(a) - f(a)) tiene un signo, y al final (g(b) - f(b)) tiene el signo contrario, entonces el Teorema de los Valores Intermedios nos dice que debe haber al menos un punto c en ese intervalo donde las dos funciones son iguales (f(c) = g(c)). Es decir, sus gráficas se cruzan.
- Encontrar las raíces de un polinomio impar
Si tienes un polinomio con un grado impar (como x³, x⁵, etc.), el Teorema de los Valores Intermedios nos ayuda a saber que siempre tendrá al menos una raíz real. Una raíz real es un número donde el polinomio vale cero. Esto es porque los polinomios de grado impar siempre van de menos infinito a más infinito (o viceversa), así que en algún momento deben cruzar el cero.
Historia del Teorema
El Teorema de los Valores Intermedios fue demostrado por primera vez por Bernard Bolzano en 1817. Más tarde, Augustin Louis Cauchy también dio una demostración en 1821. Ambos matemáticos querían hacer más precisas las ideas sobre las funciones.
La idea de que las funciones continuas tienen esta propiedad ya existía desde hace mucho tiempo. Antes de que se definiera formalmente la continuidad, a veces se pensaba que esta propiedad era parte de la definición de una función continua, o que era tan obvia que no necesitaba prueba. Bolzano y Cauchy fueron importantes porque definieron la continuidad de una manera más formal y luego demostraron el teorema basándose en esas definiciones.
Es importante saber que lo contrario del teorema no es cierto. Una función no necesita ser continua para que la conclusión del teorema de los valores intermedios se cumpla. En 1875, Jean Gaston Darboux demostró que las funciones que son derivadas de otras funciones, sean continuas o no, también tienen esta propiedad.
Véase también
 En inglés: Intermediate value theorem Facts for Kids
En inglés: Intermediate value theorem Facts for Kids
- Teorema del valor medio
- Teorema de Rolle
- Teorema del punto fijo de Brouwer