Ecuaciones de Maxwell para niños
Las ecuaciones de Maxwell son un grupo de cuatro ecuaciones muy importantes que explican cómo funcionan juntos la electricidad y el magnetismo. Imagina que son como las reglas principales que rigen estos fenómenos.
Antes de estas ecuaciones, muchos científicos como Charles-Augustin de Coulomb, Carl Friedrich Gauss, André-Marie Ampère y Michael Faraday habían descubierto leyes sobre la electricidad y el magnetismo por separado. Pero fue James Clerk Maxwell quien, en el siglo XIX, logró unirlas todas en un solo concepto: el campo electromagnético. Él añadió una idea clave llamada "corriente de desplazamiento", que ayudó a entender cómo los campos eléctricos y magnéticos se influyen mutuamente y cómo la luz es una forma de energía electromagnética.
Contenido
Historia de las Ecuaciones de Maxwell
Desde finales del siglo XVIII, muchos científicos estudiaron cómo interactúan la electricidad y el magnetismo. Descubrieron leyes como la ley de Ampère (sobre cómo las corrientes eléctricas crean campos magnéticos) y la ley de Faraday (sobre cómo los campos magnéticos cambiantes pueden generar electricidad).
Maxwell se dio cuenta de que para que la carga eléctrica se conservara (es decir, que no apareciera ni desapareciera de la nada), la ley de Ampère necesitaba un pequeño ajuste. Añadió un término que describía cómo un campo eléctrico que cambia con el tiempo puede producir un campo magnético. Esta idea, llamada "corriente de desplazamiento", fue revolucionaria.
En 1865, Maxwell publicó su trabajo A Dynamical Theory of the Electromagnetic Field. En él, predijo que existían ondas electromagnéticas que viajaban a la velocidad de la luz. Así, Maxwell demostró que la luz es una onda electromagnética, uniendo la óptica (el estudio de la luz) con el electromagnetismo.
Más tarde, en 1884, un científico llamado Oliver Heaviside, junto con Willard Gibbs, simplificó las ecuaciones de Maxwell. Las reescribió en la forma de cuatro ecuaciones que usamos hoy, utilizando una notación matemática más sencilla llamada notación vectorial. Aunque Heaviside hizo algunos cambios, las ideas fundamentales de Maxwell se mantuvieron.
Las Cuatro Ecuaciones Clave
Las ecuaciones de Maxwell son cuatro reglas matemáticas que describen cómo se comportan los campos eléctricos y magnéticos. Aquí te las explicamos de forma sencilla:
Ley de Gauss para el Campo Eléctrico
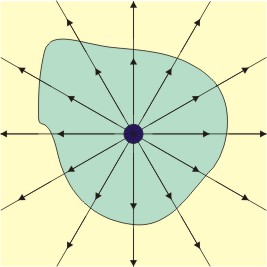
Esta ley nos dice que los campos eléctricos nacen de las cargas eléctricas. Si tienes una carga positiva, las líneas de campo eléctrico "salen" de ella. Si es una carga negativa, las líneas "entran" hacia ella.
Imagina que el campo eléctrico es como un "fluido" invisible. La ley de Gauss dice que si encierras una carga eléctrica con una superficie imaginaria (como una burbuja), la cantidad total de "fluido eléctrico" que atraviesa esa superficie depende de la cantidad de carga que hay dentro. Si no hay carga dentro, no hay "fluido" neto que entre o salga.
En matemáticas, se expresa así:
Donde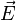 
es el campo eléctrico y 
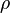es la densidad de carga (cuánta carga hay en un espacio).
Ley de Gauss para el Campo Magnético
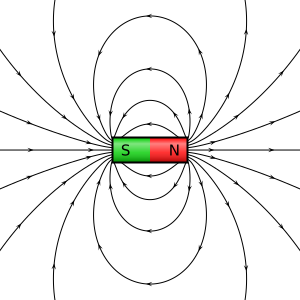
A diferencia de los campos eléctricos, los campos magnéticos no tienen "cargas" de las que salgan o a las que lleguen. Siempre forman bucles cerrados. Esto significa que no existen los "monopolos magnéticos" (un polo norte o un polo sur aislado).
Si intentaras encerrar un imán con una superficie imaginaria, verías que todas las líneas de campo magnético que salen por un lado, vuelven a entrar por el otro. Por lo tanto, el flujo magnético total a través de cualquier superficie cerrada siempre es cero.
Matemáticamente, se escribe:
Donde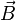 
es el campo magnético.
Ley de Faraday-Lenz
Esta ley explica cómo un campo magnético que cambia con el tiempo puede crear un campo eléctrico. Es el principio detrás de cómo funcionan los generadores eléctricos.
Imagina que tienes un circuito eléctrico y un imán. Si mueves el imán cerca del circuito, el campo magnético que lo atraviesa cambia. Este cambio genera una "fuerza electromotriz" (un voltaje) que puede hacer que la electricidad fluya por el circuito. El signo negativo en la ecuación (gracias a la ley de Lenz) nos dice que la corriente generada siempre se opone al cambio que la produce.
La forma diferencial de esta ley es:
Esto significa que un campo magnético que varía en el tiempo (Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{\partial \vec{B}}{\partial t} ) produce un campo eléctrico (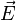) que "gira" a su alrededor.
Ley de Ampère Generalizada
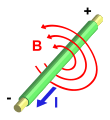
Esta ley nos dice que las corrientes eléctricas y los campos eléctricos que cambian con el tiempo pueden crear campos magnéticos. Es la base de cómo funcionan los motores eléctricos.
Originalmente, la ley de Ampère solo describía cómo una corriente eléctrica constante crea un campo magnético. Pero Maxwell añadió el término de la "corriente de desplazamiento" para incluir el efecto de los campos eléctricos que cambian.
La ecuación generalizada es:
Aquí, 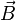es el campo magnético, 
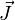es la densidad de corriente (cuánta corriente fluye por un área), y Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{\partial \vec{E}}{\partial t} es el cambio del campo eléctrico con el tiempo. Esto significa que tanto una corriente eléctrica como un campo eléctrico que cambia pueden generar un campo magnético que "gira" a su alrededor.
Las Ecuaciones de Maxwell en Resumen
Estas cuatro ecuaciones, junto con la fuerza de Lorentz (que describe cómo una carga se mueve en un campo electromagnético), son la base para entender todos los fenómenos electromagnéticos. Son compatibles con la relatividad especial de Einstein y nos ayudaron a entender que la luz es una forma de radiación electromagnética.
Aquí tienes un resumen de las cuatro ecuaciones:
| Nombre | Forma diferencial | Forma integral |
|---|---|---|
| Ley de Gauss: |  |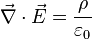
 |
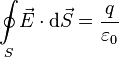| Ley de Gauss para el campo magnético: |  |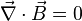
 |
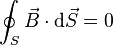| Ley de Faraday: |  |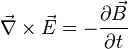
 |
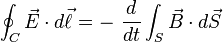| Ley de Ampère generalizada: |  |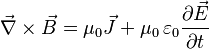
 |
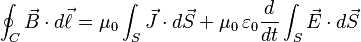Maxwell también descubrió que una cantidad que aparece en sus ecuaciones,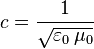 
, es exactamente la velocidad de la luz en el vacío. Esto fue una prueba más de que la luz es una onda electromagnética.
Aplicaciones en Materiales
Las ecuaciones de Maxwell también se pueden usar para describir cómo se comportan la electricidad y el magnetismo dentro de diferentes materiales, no solo en el vacío. Los materiales tienen propiedades como la permitividad eléctrica (
) y la permeabilidad magnética (
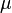), que afectan cómo los campos se propagan a través de ellos.
Por ejemplo, la permitividad eléctrica nos dice qué tan bien un material puede almacenar energía eléctrica, y la permeabilidad magnética nos dice qué tan bien un material puede soportar la formación de un campo magnético. Estas propiedades son importantes para diseñar dispositivos electrónicos y magnéticos.
Consecuencias Físicas Importantes
Conservación de la Carga
Una de las consecuencias más importantes de las ecuaciones de Maxwell es que demuestran el principio de conservación de la carga. Este principio dice que la carga eléctrica no se crea ni se destruye, solo se mueve de un lugar a otro.
Si la cantidad de carga en un lugar disminuye, significa que esa carga se ha movido y ha salido de ese lugar en forma de corriente eléctrica. Las ecuaciones de Maxwell confirman esta idea fundamental de la física.
Galería de imágenes
-
Las cuatro ecuaciones de Maxwell describen todos los fenómenos electromagnéticos.
-
Retrato de Maxwell.
Véase también
En inglés: Maxwell's equations Facts for Kids
