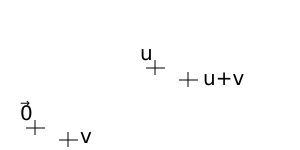Subespacio vectorial para niños
En álgebra lineal, un subespacio vectorial es como un "mini-espacio" dentro de un espacio vectorial más grande. Imagina que tienes un gran salón (el espacio vectorial) lleno de objetos que puedes mover y combinar. Un subespacio vectorial sería una parte de ese salón, como una sección especial, donde los objetos siguen las mismas reglas de movimiento y combinación que en todo el salón.
Para que una parte sea un subespacio vectorial, debe cumplir ciertas condiciones. Esto significa que si tomas cualquier "objeto" de esa sección y lo combinas con otro "objeto" de la misma sección, el resultado debe seguir estando dentro de esa sección. Lo mismo ocurre si "estiras" o "encoges" un objeto de esa sección; el resultado debe permanecer allí.
Contenido
¿Qué es un subespacio vectorial?
Un subespacio vectorial es un conjunto de elementos (llamados vectores) que forman parte de un espacio vectorial más grande. Para que este conjunto más pequeño sea un subespacio, debe cumplir dos reglas importantes:
- Regla 1: La suma se queda dentro. Si tomas dos vectores cualquiera de este subconjunto y los sumas, el resultado de esa suma también debe ser un vector que pertenezca al mismo subconjunto.
- Regla 2: La multiplicación por un número se queda dentro. Si tomas un vector de este subconjunto y lo multiplicas por cualquier número (real o complejo, dependiendo del tipo de espacio), el resultado de esa multiplicación también debe ser un vector que pertenezca al mismo subconjunto.
Además, el subconjunto no debe estar vacío; siempre debe contener al menos el vector nulo (el "cero" del espacio vectorial).
¿Por qué son importantes estas reglas?
Estas dos reglas aseguran que el subconjunto se comporte como un espacio vectorial por sí mismo. Si se cumplen, significa que puedes hacer todas las operaciones básicas (sumar, restar, multiplicar por números) dentro de ese subconjunto sin salirte de él.
Por ejemplo, el vector nulo (el "cero") siempre debe estar en un subespacio. Esto se puede ver si multiplicas cualquier vector del subespacio por el número cero. El resultado será el vector nulo, y por la Regla 2, debe estar en el subespacio.
Una forma más sencilla de verificarlo
Podemos combinar las dos reglas en una sola para que sea más fácil verificar si un conjunto es un subespacio:
Si tienes un espacio vectorial grande V, un subconjunto U (que no esté vacío) es un subespacio vectorial si, al tomar dos vectores cualesquiera de U (llamémoslos v y w) y dos números cualesquiera (llamémoslos r y s), la combinación r veces v más s veces w (es decir, rv + sw) también es un elemento de U.
Ejemplos de subespacios
Vamos a usar el espacio vectorial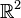 
, que puedes imaginar como un plano con puntos (x,y).
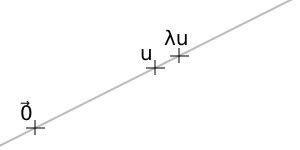
- Ejemplo 1: Una línea recta que pasa por el origen.
Considera el conjunto de todos los puntos (a,b) en el plano donde la suma de sus coordenadas es cero (a+b=0). Esto significa que los puntos son de la forma (a, -a), como (1,-1), (2,-2), (0,0), etc. Estos puntos forman una línea recta que pasa por el origen (0,0). * Si sumas dos puntos de esta línea, por ejemplo (1,-1) y (2,-2), obtienes (3,-3). La suma de sus coordenadas (3 + (-3)) es 0, así que el resultado sigue en la línea. * Si multiplicas un punto de esta línea por un número, por ejemplo 2 * (1,-1) = (2,-2). La suma de sus coordenadas (2 + (-2)) es 0, así que el resultado sigue en la línea. * El punto (0,0) está en la línea (0+0=0). Por lo tanto, este conjunto es un subespacio vectorial.
- Ejemplo 2: Una curva que no pasa por el origen o no es recta.
Considera el conjunto de todos los puntos (a,b) donde b es igual a a al cuadrado (b = a²). Por ejemplo, (1,1), (2,4), (0,0), (-1,1). Esto forma una curva llamada parábola. * El punto (0,0) sí está en la curva (0 = 0²). * Pero si sumas dos puntos de la curva, por ejemplo (1,1) y (2,4), obtienes (3,5). Para que (3,5) esté en la curva, 5 debería ser igual a 3², lo cual no es cierto (3²=9). Así que la suma no se queda en la curva. * Si multiplicas un punto de la curva por un número, por ejemplo 2 * (2,4) = (4,8). Para que (4,8) esté en la curva, 8 debería ser igual a 4², lo cual no es cierto (4²=16). Así que la multiplicación no se queda en la curva. Por lo tanto, este conjunto NO es un subespacio vectorial.
Otros ejemplos de subespacios
- El subespacio más pequeño: El conjunto que solo contiene el vector nulo (el "cero" del espacio) es siempre un subespacio. Se le llama el subespacio trivial.
- El subespacio más grande: El espacio vectorial completo V es siempre un subespacio de sí mismo.
- Líneas y planos que pasan por el origen: En un espacio tridimensional, cualquier línea recta o cualquier plano que pase por el punto (0,0,0) es un subespacio vectorial.
Cómo combinar subespacios
Podemos hacer operaciones con subespacios para crear nuevos subconjuntos.
Unión de subespacios
La unión de dos subespacios (S y W) es el conjunto de todos los vectores que están en S, o en W, o en ambos. En general, la unión de dos subespacios NO es siempre un subespacio.
Intersección de subespacios
La intersección de dos subespacios (S y W) es el conjunto de todos los vectores que están en S Y en W al mismo tiempo. La intersección de dos subespacios SIEMPRE es un subespacio.
Suma de subespacios
La suma de dos subespacios (S y W) es el conjunto de todos los vectores que se pueden formar sumando un vector de S con un vector de W. La suma de dos subespacios SIEMPRE es un subespacio.
Suma directa
Si la única forma en que dos subespacios S y W se "cruzan" es en el vector nulo (es decir, su intersección es solo el vector cero), entonces a su suma se le llama "suma directa". Esto es importante porque significa que cada vector en la suma directa se puede escribir de una única manera como la suma de un vector de S y un vector de W.
Subespacios suplementarios
Dos subespacios S y W son "suplementarios" si su suma directa es igual a todo el espacio vectorial original V. Esto significa que juntos "llenan" todo el espacio, y solo se superponen en el vector nulo.
Dimensiones de subespacios
La "dimensión" de un subespacio es como el número de "direcciones" independientes que tiene. Por ejemplo, una línea tiene dimensión 1, un plano tiene dimensión 2, y el espacio tridimensional tiene dimensión 3.
Existe una fórmula llamada la fórmula de Grassmann que nos ayuda a calcular la dimensión de la suma de dos subespacios: 
Esto significa que la dimensión de la suma de S y W es igual a la dimensión de S, más la dimensión de W, menos la dimensión de su intersección.
Por ejemplo, si S tiene dimensión 3 y W tiene dimensión 2, y su intersección tiene dimensión 1, entonces la dimensión de su suma será 3 + 2 - 1 = 4.
En la suma directa
Cuando tenemos una suma directa, la intersección de los subespacios es solo el vector nulo, que tiene dimensión 0. En este caso, la fórmula de Grassmann se simplifica: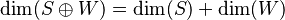 
Así, la dimensión de la suma directa es simplemente la suma de las dimensiones de los subespacios individuales.
Galería de imágenes
-
El vector nulo, un vector u y el resultado de multiplicar u por un número (λu) siempre están en la misma línea si el subespacio es una línea que pasa por el origen.
-
Si sumas dos vectores u y v en un subespacio, el resultado u+v también debe estar en el subespacio.
-
La suma de varios elementos también debe permanecer en el subespacio.
Véase también
En inglés: Linear subspace Facts for Kids
- Base (álgebra)
- Combinación lineal
- Dependencia e independencia lineal
- Espacio vectorial
- Producto escalar
- Producto vectorial
- Producto mixto
- Sistema generador
