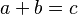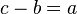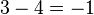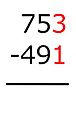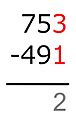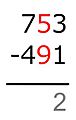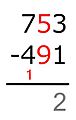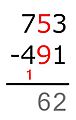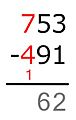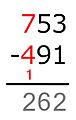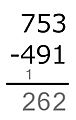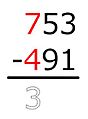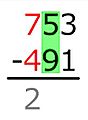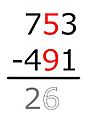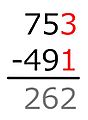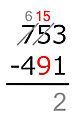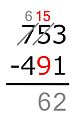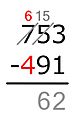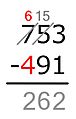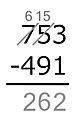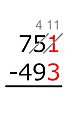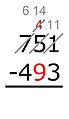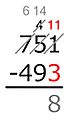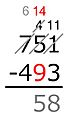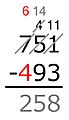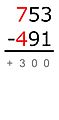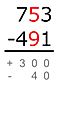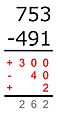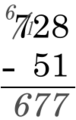Resta para niños

La resta o sustracción es una operación matemática que se usa para quitar una cantidad de otra. Se representa con el signo de menos (−). Por ejemplo, si tienes 5 manzanas y quitas 2, te quedan 3 manzanas. Esto se escribe como 5 − 2 = 3.

La resta se puede aplicar a muchos tipos de números, como los números enteros (positivos y negativos), las fracciones, los números decimales y más.

Algunas reglas importantes de la resta son:

• No es lo mismo restar un número que el otro. Por ejemplo, 5 − 2 es 3, pero 2 − 5 es -3. Esto se llama ser anticonmutativa.
• El orden importa cuando restas más de dos números. Por ejemplo, (10 − 3) − 2 no es lo mismo que 10 − (3 − 2). Esto significa que no es asociativa.
• Restar 0 a un número no cambia el número. Por ejemplo, 7 − 0 = 7.

La resta está muy relacionada con la suma y la multiplicación.

La resta en los primeros años

«5 − 2 = 3» (verbalmente, «cinco menos dos es igual a tres»).

Desde pequeños, los niños aprenden a entender la idea de quitar y poner objetos. Esto les ayuda a comprender la suma y la resta. Por ejemplo, si un niño tiene 6 canicas y le quitan 1, sabe que ahora tiene 5. Aquí, 6 es la cantidad inicial, quitar 1 es la transformación, y 5 es la cantidad final.

Restar números pequeños es una de las primeras cosas que se aprenden en matemáticas. En la educación primaria, los estudiantes aprenden a restar números en el sistema decimal, empezando con números de un solo dígito y luego con problemas más complejos. Para ayudar a restar, se han usado herramientas desde el antiguo ábaco hasta las computadoras modernas.

Resta con números enteros

Imagina una línea recta. Si empiezas en un punto a y te mueves b pasos a la derecha para llegar a c, esto se representa con una suma:

Si desde c te mueves b pasos a la izquierda para volver a a, esto se representa con una resta:

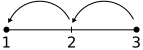
Si tienes una línea con los números 1, 2 y 3:

• Desde el 3, si no das ningún paso a la izquierda, sigues en el 3. Así, 3 − 0 = 3.
• Si das 2 pasos a la izquierda desde el 3, llegas al 1. Así, 3 − 2 = 1.

Para restar cualquier número natural, usamos una línea que contiene todos los números naturales (0, 1, 2, 3, ...). Desde el 3, si das 3 pasos a la izquierda, llegas al 0. Así, 3 − 3 = 0. Pero si intentas restar 4 a 3 (3 − 4), te sales de la línea de números naturales, porque el resultado sería un número negativo.

Para resolver esto, usamos la línea numérica de los números enteros (..., -3, -2, -1, 0, 1, 2, 3, ...). Así, desde el 3, si das 4 pasos a la izquierda, llegas al -1:

Cartel exterior de tienda en Burdeos publicitando descuentos del 20% del precio de un segundo perfume

Resta como suma de números con signo

A veces, la resta puede ser un poco confusa, como cuando restamos un número negativo. Por ejemplo, ¿qué significa 3 − (-2)? No es fácil imaginar quitar "-2 manzanas".

Una forma de entenderlo es ver la resta como una suma de números con signo. El signo menos antes de un número negativo significa que se convierte en su opuesto positivo. Así, 3 − (-2) se convierte en 3 + 2, que es igual a 5.

Esto simplifica las matemáticas, ya que no necesitamos una operación de resta separada. En lugar de eso, usamos la suma y el concepto de números opuestos.

Algoritmos para restar

Los algoritmos son pasos o reglas que nos ayudan a resolver problemas matemáticos de manera eficiente. Los algoritmos para sumar, restar, multiplicar y dividir fueron desarrollados gracias al trabajo de Mohamed ibn Musa Al’khwarizmi (780 a 850 d.C.), quien combinó la numeración hindú, el valor posicional y el concepto del cero.

Existen varios métodos para restar, y cada uno es útil para diferentes situaciones. Para calcular a mano, se usan distintos métodos. Por ejemplo, al dar cambio en una tienda, a veces no se hace una resta directa, sino que se cuenta hacia arriba desde el precio hasta el dinero entregado.

Para las computadoras, se usa un método llamado "método de complementos", donde la resta se convierte en una suma en un sistema especial de números.

Cómo se enseña la resta en las escuelas

Los métodos para enseñar la resta en la escuela primaria varían mucho entre países y a lo largo del tiempo.

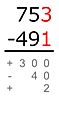
Algunas escuelas en Europa usan un método llamado "método austriaco" o "método de adiciones". En este método, no se "pide prestado" a la siguiente columna. En cambio, se usan pequeñas marcas para recordar los cambios.

Este método descompone la resta en pasos, restando dígito por dígito según su valor posicional. Se empieza por la derecha (las unidades). Por ejemplo, para restar un número como s_js_j-1...s₁ (el sustraendo) de otro número como m_km_k-1...m₁ (el minuendo), donde cada s_i y m_i es un dígito: Se resta m₁ − s₁, luego m₂ − s₂, y así sucesivamente, siempre que el dígito de arriba (minuendo) sea igual o mayor que el de abajo (sustraendo). Si el dígito de arriba es menor, se le suma 10. Para corregir este aumento, el método americano reduce el siguiente dígito del minuendo en uno (se "pide prestado"). El método europeo, en cambio, aumenta el siguiente dígito del sustraendo en uno.

Ejemplo: 704 − 512.

El minuendo es 704 y el sustraendo es 512.

• En las unidades: 4 no es menor que 2, así que 4 − 2 = 2. Se escribe 2 en el resultado.
• En las decenas: 0 es menor que 1. Se le suma 10 al 0, convirtiéndolo en 10. Ahora, 10 − 1 = 9. Se escribe 9 en el resultado.

* En el método americano, para compensar el "préstamo" de 10, se reduce el dígito de las centenas del minuendo (el 7) en uno, convirtiéndolo en 6.

• En las centenas: Ahora se resta 6 − 5 = 1. Se escribe 1 en el resultado.

El resultado final es 192.

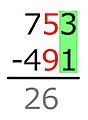
El método austriaco no cambia el 7 a 6. En su lugar, aumenta el dígito de las centenas del sustraendo (el 5) en uno (lo que se marca con una pequeña señal). Luego, se piensa: ¿qué número, al sumarle 1 (del aumento) y luego 5, da 7? La respuesta es 1, y ese es el dígito que se anota en las centenas.

Resta a mano

Método austriaco

Este método se enfoca en sumar para encontrar la diferencia.

• 

  1 + … = 3

• 

  Se escribe la diferencia debajo de la línea.

• 

  9 + … = 5
  ¡La suma requerida (5) es demasiado pequeña!

• 

  Por lo tanto, añadimos 10 a la misma y ponemos un 1 bajo el siguiente lugar más alto en el sustraendo.

• 

  9 + … = 15
  Ahora podemos ver la diferencia como antes.

• 

  (4 + 1) + … = 7

• 

  Se escribe la diferencia debajo de la línea.

• 

  Se escribe la diferencia total.

Resta de izquierda a derecha

En este método, se empieza a restar desde el dígito más grande (izquierda) y se ajusta si es necesario.

• 

  7 − 4 = 3
  Este resultado solo se dibuja con lápiz aquí.

• 

  Debido a que el siguiente dígito del minuendo es menor que el sustraendo, se resta uno de nuestro con lápiz-en-número y mentalmente se añade diez a la siguiente.

• 

  15 − 9 = 6

• 

  Debido a que el siguiente dígito del minuendo no es menor que el sustraendo, se mantiene este número.

• 

  3 − 1 = 2

Método americano

Este método implica "pedir prestado" de la columna de la izquierda cuando el dígito de arriba es más pequeño.

• 

  3 − 1 = …

• 

  Se escribe la diferencia debajo de la línea.

• 

  5 − 9 = …
  ¡El minuendo (5) es demasiado pequeño!

• 

  Por lo tanto, se le suma 10 al mismo. El 10 es 'prestado' del dígito de la izquierda, el cual baja en 1.

• 

  15 − 9 = …
  Ahora la resta funciona, y escribimos la diferencia debajo de la línea.

• 

  6 − 4 = …

• 

  Se escribe la diferencia debajo de la línea.

• 

  La diferencia total.

Primero comercio

Una variación del método americano donde todos los "préstamos" se hacen antes de empezar a restar.

• 

  1 − 3 = no es posible.
  Añadimos un 10 al 1. Debido a que el 10 es «prestado» desde el 5 cercano, el 5 se baja en 1.

• 

  4 − 9 = no es posible.
  Así se procede como en el paso 1.

• 

  Trabajando de derecha a izquierda:
  11 − 3 = 8

• 

  14 − 9 = 5

• 

  6 − 4 = 2

Diferencias parciales

Este método no usa "préstamos". En su lugar, se restan los dígitos y se anota si la diferencia es positiva o negativa, y luego se suman todas las diferencias.

• 

  El número menor se resta del mayor:
  700 − 400 = 300
  Debido a que el minuendo es mayor que el sustraendo, esta diferencia tiene un signo de más.

• 

  El número menor se resta del mayor:
  90 − 50 = 40
  Debido a que el minuendo es menor que el sustraendo, esta diferencia tiene un signo de menos.

• 

  El número menor se resta del mayor:
  3 − 1 = 2
  Debido a que el minuendo es mayor que el sustraendo, esta diferencia tiene un signo de más.

• 

  + 300 − 40 + 2 = 262

Métodos no verticales

Contando hacia arriba

En lugar de restar dígito por dígito, puedes contar desde el número más pequeño (sustraendo) hasta el más grande (minuendo), sumando los pasos.

Ejemplo: Para 1234 − 567, puedes hacer:

• 567 + 3 = 570
• 570 + 30 = 600
• 600 + 400 = 1000
• 1000 + 234 = 1234

Luego, sumas los pasos: 3 + 30 + 400 + 234 = 667.

Dividiendo la resta

Otro método útil para calcular mentalmente es dividir la resta en pasos más pequeños.

Ejemplo: Para 1234 − 567, puedes hacer:

• 1234 − 500 = 734
• 734 − 60 = 674
• 674 − 7 = 667

Igual cambio

Este método se basa en que si sumas o restas el mismo número al minuendo y al sustraendo, la respuesta no cambia. Se añade una cantidad para que el sustraendo termine en ceros, lo que facilita la resta.

Ejemplo: Para 1234 − 567, puedes hacer:

• 1234 − 567 = 1237 − 570 (sumamos 3 a ambos) = 1267 − 600 (sumamos 30 a ambos) = 667

Resta de unidades de medida

Cuando restas dos números que tienen unidades de medida (como kilogramos o metros), las unidades deben ser las mismas. En la mayoría de los casos, el resultado tendrá la misma unidad que los números originales.

Una excepción es cuando restas porcentajes. La diferencia se expresa en "puntos porcentuales". Por ejemplo, si algo cambia del 20% al 15%, la diferencia es de 5 puntos porcentuales.

Tabla de restar

Sustracción de números 0-10. Línea etiqueta = minuendo. eje X = sustraendo. eje Y = diferencia.

Así como hay tablas de multiplicar, también hay tablas de restar que muestran los resultados de las restas básicas.

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \begin{array}{c} tabla \; de \; restar \\ \\ \begin{array}{ccccc} \begin{array}{|c|} \hline tabla \; del \; 1 \\ \begin{array}{rcrcr} 1 & - & 0 & = & 1 \\ 1 & - & 1 & = & 0 \\ \end{array} \\ \hline \end{array} & \begin{array}{|c|} \hline tabla \; del \; 2 \\ \begin{array}{rcrcr} 2 & - & 0 & = & 2 \\ 2 & - & 1 & = & 1 \\ 2 & - & 2 & = & 0 \\ \end{array} \\ \hline \end{array} & \begin{array}{|c|} \hline tabla \; del \; 3 \\ \begin{array}{rcrcr} 3 & - & 0 & = & 3 \\ 3 & - & 1 & = & 2 \\ 3 & - & 2 & = & 1 \\ 3 & - & 3 & = & 0 \\ \end{array} \\ \hline \end{array} & \begin{array}{|c|} \hline tabla \; del \; 4 \\ \begin{array}{rcrcr} 4 & - & 0 & = & 4 \\ 4 & - & 1 & = & 3 \\ 4 & - & 2 & = & 2 \\ 4 & - & 3 & = & 1 \\ 4 & - & 4 & = & 0 \\ \end{array} \\ \hline \end{array} & \begin{array}{|c|} \hline tabla \; del \; 5 \\ \begin{array}{rcrcr} 5 & - & 0 & = & 5 \\ 5 & - & 1 & = & 4 \\ 5 & - & 2 & = & 3 \\ 5 & - & 3 & = & 2 \\ 5 & - & 4 & = & 1 \\ 5 & - & 5 & = & 0 \\ \end{array} \\ \hline \end{array} \\ \\ \begin{array}{|c|} \hline tabla \; del \; 6 \\ \begin{array}{rcrcr} 6 & - & 0 & = & 6 \\ 6 & - & 1 & = & 5 \\ 6 & - & 2 & = & 4 \\ 6 & - & 3 & = & 3 \\ 6 & - & 4 & = & 2 \\ 6 & - & 5 & = & 1 \\ 6 & - & 6 & = & 0 \\ \end{array} \\ \hline \end{array} & \begin{array}{|c|} \hline tabla \; del \; 7 \\ \begin{array}{rcrcr} 7 & - & 0 & = & 7 \\ 7 & - & 1 & = & 6 \\ 7 & - & 2 & = & 5 \\ 7 & - & 3 & = & 4 \\ 7 & - & 4 & = & 3 \\ 7 & - & 5 & = & 2 \\ 7 & - & 6 & = & 1 \\ 7 & - & 7 & = & 0 \\ \end{array} \\ \hline \end{array} & \begin{array}{|c|} \hline tabla \; del \; 8 \\ \begin{array}{rcrcr} 8 & - & 0 & = & 8 \\ 8 & - & 1 & = & 7 \\ 8 & - & 2 & = & 6 \\ 8 & - & 3 & = & 5 \\ 8 & - & 4 & = & 4 \\ 8 & - & 5 & = & 3 \\ 8 & - & 6 & = & 2 \\ 8 & - & 7 & = & 1 \\ 8 & - & 8 & = & 0 \\ \end{array} \\ \hline \end{array} & \begin{array}{|c|} \hline tabla \; del \; 9 \\ \begin{array}{rcrcr} 9 & - & 0 & = & 9 \\ 9 & - & 1 & = & 8 \\ 9 & - & 2 & = & 7 \\ 9 & - & 3 & = & 6 \\ 9 & - & 4 & = & 5 \\ 9 & - & 5 & = & 4 \\ 9 & - & 6 & = & 3 \\ 9 & - & 7 & = & 2 \\ 9 & - & 8 & = & 1 \\ 9 & - & 9 & = & 0 \\ \end{array} \\ \hline \end{array} & \begin{array}{|c|} \hline tabla \; del \; 10 \\ \begin{array}{rcrcr} 10 & - & 0 & = & 10 \\ 10 & - & 1 & = & 9 \\ 10 & - & 2 & = & 8 \\ 10 & - & 3 & = & 7 \\ 10 & - & 4 & = & 6 \\ 10 & - & 5 & = & 5 \\ 10 & - & 6 & = & 4 \\ 10 & - & 7 & = & 3 \\ 10 & - & 8 & = & 2 \\ 10 & - & 9 & = & 1 \\ 10 & - & 10 & = & 0 \\ \end{array} \\ \hline \end{array} \\ \end{array} \\ \end{array>

Galería de imágenes

• 

  Un problema de ejemplo

Véase también

En inglés: Subtraction Facts for Kids

• Aritmética
• Número negativo
• Diferencia de conjuntos