Tensión cortante para niños
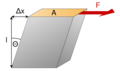
La tensión cortante o tensión de cizalla es un tipo de fuerza que actúa sobre un objeto de una manera muy específica. Imagina que tienes un sándwich y lo empujas con una mano hacia adelante y con la otra hacia atrás. Esa fuerza que intenta "cortar" o "deslizar" las capas del sándwich es la tensión cortante.
En ingeniería y física, esta tensión se representa con la letra griega tau (τ). Aparece en objetos largos, como vigas o columnas, cuando se les aplica una fuerza que intenta cortarlos o torcerlos. A diferencia de otras fuerzas que estiran o comprimen un objeto, la tensión cortante actúa de forma paralela a la superficie del material.
Contenido
¿Cómo se calcula la tensión cortante promedio?
Calcular la tensión cortante no es tan sencillo porque la fuerza no se distribuye de manera uniforme en toda la superficie. Sin embargo, podemos calcular una tensión cortante promedio. Para esto, usamos una fórmula simple:
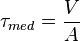
Aquí, V es la fuerza cortante total que se aplica, y A es el área de la superficie sobre la cual se aplica esa fuerza.
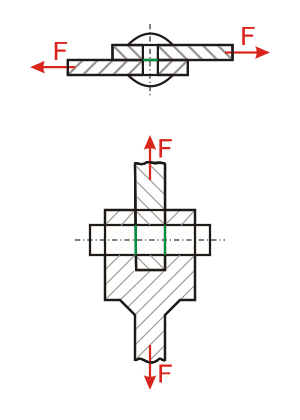
Piensa en un tornillo que une dos piezas (como en la Fig 2.). Si las piezas se mueven en direcciones opuestas, el tornillo sufre una tensión cortante que intenta "cortarlo" por la mitad. La línea verde en la imagen muestra dónde actúa esta fuerza de corte.
La fórmula de Collignon-Jourawski
Cuando necesitamos saber la tensión cortante en un punto muy específico de una viga, por ejemplo, usamos una fórmula más avanzada. Esta fórmula es conocida como la fórmula de Collignon, aunque también fue desarrollada por el ingeniero ruso D. J. Jourawski en 1844.
La fórmula se ve así: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \bar{\tau}_{xy} = \frac {V_y(x) m_z(y)}{I_z t_z(y)}
No te preocupes si parece complicada. Lo importante es saber que:
- Vy es la fuerza cortante.
- mz es el primer momento de área parcial, que tiene que ver con la forma de la sección del objeto.
- Iz es el momento de inercia de toda la sección, que nos dice cómo se distribuye la masa del objeto.
- tz es el grosor del objeto en el punto donde queremos calcular la tensión.
Esta fórmula nos ayuda a entender cómo se distribuye la tensión cortante en una viga. Por ejemplo, nos dice que:
- La tensión cortante es cero en los bordes superior e inferior de la viga.
- La tensión cortante suele ser máxima en el centro de la viga, en una línea imaginaria llamada "línea neutra".
¿Cuál es la tensión cortante máxima?
La tensión cortante máxima es el punto donde el material experimenta la mayor fuerza de corte. Es importante conocerla para asegurar que una estructura sea segura y no se rompa.
Podemos relacionar la tensión máxima con la tensión promedio usando un factor llamado ksec: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \tau_{max} = k_{sec} \cdot \tau_{med} Este factor ksec siempre es igual o mayor que 1.
Para una sección rectangular
Imagina una viga con forma de rectángulo. Si aplicamos una fuerza de corte, la tensión máxima será 1.5 veces la tensión promedio. Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \bar{\tau}_{max} = \frac{3}{2}\tau_{med}
Para una sección circular
Si la viga tiene forma de círculo, la tensión máxima será aproximadamente 1.33 veces la tensión promedio. Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \bar{\tau}_{max} = \frac{4}{3}\tau_{med}
Para una sección doble T
Las vigas con forma de "doble T" son muy comunes en la construcción. En estas, la tensión máxima se encuentra en la parte central, llamada "alma". Calcularla es un poco más complejo, pero los ingenieros usan fórmulas para asegurarse de que estas vigas sean muy resistentes.
Galería de imágenes
Véase también
 En inglés: Shear stress Facts for Kids
En inglés: Shear stress Facts for Kids
- Módulo de cizalladura
- Esfuerzo interno
- Esfuerzo cortante
- Centro de cortante y torsión
- Tensión mecánica