Plasticidad (mecánica de sólidos) para niños
La plasticidad es una característica de algunos materiales que les permite cambiar de forma de manera permanente. Imagina que estiras una banda elástica: vuelve a su forma original. Eso es elasticidad. Pero si doblas un clip de papel, se queda doblado. Eso es plasticidad.
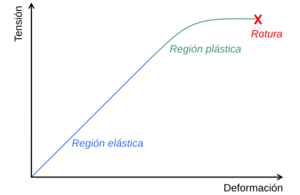
Cuando un material se deforma plásticamente, no regresa a su forma inicial, incluso si la fuerza que lo deformó desaparece. Esto ocurre cuando la fuerza es mayor que un punto llamado "límite elástico".
Contenido
¿Qué es la plasticidad en los materiales?
Muchos materiales, como los metales, pueden estirarse o doblarse un poco y volver a su forma original. Esto se llama comportamiento elástico. Es como un muelle: lo estiras y vuelve. Pero si aplicas demasiada fuerza, el material puede deformarse de forma permanente. Esto significa que, aunque quites la fuerza, el material no recupera su forma inicial. A este cambio permanente lo llamamos deformación plástica.
Existe un punto clave llamado límite elástico. Si la fuerza aplicada supera este límite, el material empieza a deformarse de forma plástica. Es decir, el cambio ya no es reversible.
Algunos materiales, como la arcilla o la plastilina, son muy plásticos. Se deforman permanentemente con muy poca fuerza. Otros materiales, como algunos metales, pueden volverse más duros a medida que se deforman plásticamente. Esto se conoce como plasticidad con endurecimiento.
¿Por qué los metales son plásticos?
En los metales, la plasticidad ocurre debido a pequeños defectos en su estructura interna, llamados dislocaciones. Piensa en los átomos de un metal como ladrillos apilados. A veces, hay un ladrillo que no está perfectamente alineado. Cuando aplicas una fuerza, estos "ladrillos desalineados" se mueven, causando un cambio permanente en la forma del metal.
La historia del estudio de la plasticidad
El estudio de cómo los materiales se deforman plásticamente comenzó hace mucho tiempo. En el siglo XIX, científicos como Tresca y Saint-Venant sentaron las bases de lo que hoy conocemos sobre la plasticidad. Ellos empezaron a entender que los materiales podían deformarse de forma irreversible.
A principios del siglo XX, otros investigadores como Prandtl y Von Mises hicieron más avances. Introdujeron ideas importantes como la deformación permanente y cómo los materiales se endurecen al deformarse.
Después de la Segunda Guerra Mundial, científicos como Prager y Hill mejoraron las fórmulas matemáticas para describir la plasticidad. Esto ayudó a entender mejor cómo se comportan los materiales bajo diferentes fuerzas.
¿Cómo se usa la plasticidad en la ingeniería?
La plasticidad es muy importante en la ingeniería, especialmente al diseñar estructuras como edificios y puentes.
Plasticidad en estructuras de metal
Cuando se construyen estructuras de metal, los ingenieros usan el concepto de plasticidad para asegurarse de que sean seguras y resistentes. Aunque las estructuras deben ser elásticas para soportar las cargas diarias, en situaciones extremas (como un terremoto), es útil que puedan deformarse plásticamente sin romperse de inmediato.
Imagina una viga de metal. Si se le aplica mucha fuerza, puede que se doble permanentemente en ciertos puntos. Estos puntos se llaman "rótulas plásticas". Es como si la viga creara una articulación para liberar la tensión. Los ingenieros calculan dónde y cuándo aparecerán estas rótulas para diseñar estructuras que puedan soportar cargas muy grandes antes de colapsar. Esto permite que las estructuras aprovechen al máximo la resistencia de los materiales.
Plasticidad en el hormigón armado
El hormigón armado es una mezcla de hormigón y barras de acero. El acero dentro del hormigón también se deforma plásticamente. Cuando las barras de acero se estiran mucho, pueden endurecerse y soportar aún más fuerza. Esto es muy útil porque permite usar menos acero en las construcciones, haciendo que sean más económicas sin perder seguridad.
Plasticidad en los suelos
La plasticidad no solo se ve en metales, ¡también en la tierra! En el caso de algunos suelos húmedos, la plasticidad es la capacidad de ser moldeados y mantener esa forma, incluso cuando se secan. Piensa en la arcilla: puedes darle forma y, al secarse, la mantiene.
No todos los suelos son igual de plásticos. Las arenas y los limos tienen muy poca plasticidad, mientras que los suelos con mucha arcilla son muy plásticos. Un suelo con menos del 15% de arcilla generalmente no es plástico.
Límites de plasticidad de los suelos
Los científicos han definido dos "límites de plasticidad" para los suelos:
- Límite máximo de plasticidad: Si un suelo tiene más humedad que este límite, se vuelve líquido y no puede mantener su forma.
- Límite mínimo de plasticidad: Si un suelo tiene menos humedad que este límite, se vuelve quebradizo y no se puede moldear.
La diferencia entre el porcentaje de humedad de estos dos límites se llama índice de plasticidad. Este índice nos dice qué tan plástico es un suelo. Los suelos con más arcilla suelen tener un índice de plasticidad más alto.
Otros factores, como los tipos de sales (cationes) presentes en el suelo y la cantidad de materia orgánica, también influyen en su plasticidad. Por ejemplo, los suelos con más materia orgánica (como los de la superficie) suelen ser más plásticos.
Galería de imágenes
Véase también
 En inglés: Plasticity (physics) Facts for Kids
En inglés: Plasticity (physics) Facts for Kids