Vértice (teoría de grafos) para niños
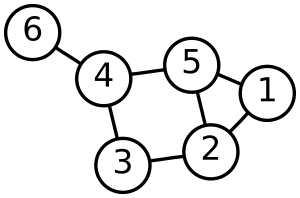
En la teoría de grafos, un vértice (también llamado nodo) es como un punto o un lugar en un mapa. Es la parte más básica de la que se forman los grafos. Imagina un grafo como una red de caminos o conexiones.
Un grafo puede ser de dos tipos:
- Un grafo no dirigido tiene vértices y aristas. Las aristas son como caminos que conectan dos vértices sin importar la dirección. Piensa en una amistad: si tú eres amigo de alguien, esa persona también es tu amigo.
- Un grafo dirigido tiene vértices y arcos. Los arcos son como caminos que van en una sola dirección. Por ejemplo, si sigues a alguien en una red social, esa persona no necesariamente te sigue a ti.
Los vértices son como puntos simples. No tienen propiedades especiales por sí mismos. Sin embargo, en algunos casos, pueden representar cosas importantes. Por ejemplo, en una red de ideas, los vértices pueden ser conceptos o tipos de objetos.
Los dos vértices que una arista conecta se llaman puntos finales de esa arista. Se dice que la arista es incidente a esos vértices. Si un vértice W está conectado a otro vértice V por una arista, decimos que W es adyacente a V. La vecindad de un vértice V incluye a todos los vértices que están conectados directamente a V.
Contenido
- Vértices en los Grafos: Los Puntos Clave
- Galería de imágenes
- Véase también
Vértices en los Grafos: Los Puntos Clave
¿Qué son los Vértices y las Aristas?
Los vértices son los "puntos" o "nodos" de un grafo. Son las unidades fundamentales. Las aristas (o arcos en grafos dirigidos) son las "líneas" que conectan estos puntos. Juntos, forman la estructura de un grafo.
Cómo se Conectan los Vértices: Adyacencia y Vecindad
Cuando dos vértices están unidos por una arista, se dice que son adyacentes. Es como si fueran vecinos. La vecindad de un vértice incluye a todos sus vecinos directos. Por ejemplo, si tu casa es un vértice, tus vecinos más cercanos son parte de tu vecindad.
El Grado de un Vértice: ¿Cuántas Conexiones Tiene?
El grado de un vértice nos dice cuántas aristas están conectadas a él. Es como contar cuántos caminos salen de un punto.
Tipos Especiales de Vértices por su Grado
- Un vértice aislado es un vértice que no tiene ninguna conexión. Su grado es cero. Es como una isla sin puentes.
- Un vértice hoja es un vértice que solo tiene una conexión. Su grado es uno. Piensa en la hoja de un árbol que está unida a una sola rama.
- En los grafos dirigidos, podemos hablar de:
* Grado de salida: Cuántos arcos "salen" del vértice. * Grado de entrada: Cuántos arcos "llegan" al vértice.
- Un vértice fuente es un vértice del que solo salen arcos (su grado de entrada es cero).
- Un sumidero es un vértice al que solo llegan arcos (su grado de salida es cero).
Vértices que Afectan la Conexión del Grafo
Algunos vértices son muy importantes para mantener unido un grafo:
- Un vértice de corte es un vértice que, si lo quitas, el grafo se divide en dos o más partes separadas. Es como un puente clave que, si se derrumba, aísla una zona.
- Un conjunto independiente es un grupo de vértices donde ninguno está conectado directamente con otro.
- Una cobertura de vértices es un grupo de vértices que "cubren" todas las aristas del grafo. Esto significa que cada arista tiene al menos uno de sus puntos finales en este grupo.
Vértices con Etiquetas: ¿Son Todos Iguales?
A veces, los vértices pueden tener etiquetas. Estas etiquetas son como nombres o información extra que los hacen únicos.
- Los vértices etiquetados tienen información adicional que los distingue. Si dos grafos son iguales, sus vértices etiquetados deben coincidir.
- Los vértices no etiquetados son más genéricos. Se pueden intercambiar con otros vértices si tienen las mismas conexiones.
¿Por qué son Importantes las Etiquetas?
Las etiquetas son importantes cuando queremos saber si dos grafos son exactamente iguales (a esto se le llama isomorfismo de grafos). Si los vértices tienen etiquetas, deben coincidir para que los grafos sean idénticos. Si no tienen etiquetas, solo nos fijamos en cómo están conectados.
Galería de imágenes
Véase también
 En inglés: Graph (mathematics) Facts for Kids
En inglés: Graph (mathematics) Facts for Kids