Regla de la cadena para niños

Enciclopedia para niños

La regla de la cadena es una herramienta muy importante en matemáticas, especialmente en el área del análisis. Nos ayuda a calcular la derivada de una función compuesta. Imagina que tienes una función que depende de otra función. La regla de la cadena te dice cómo encontrar la tasa de cambio de la primera función con respecto a la variable de la segunda.

Piensa en esto como una cadena: si una variable y depende de una segunda variable u, y a su vez u depende de una variable x, entonces la regla de la cadena te permite saber cómo cambia y cuando x cambia. Es como multiplicar las tasas de cambio: la tasa de cambio de y respecto a u, multiplicada por la tasa de cambio de u respecto a x.

En símbolos, si tenemos:

y que depende de u
u que depende de x

La regla de la cadena se ve así: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac {\mathrm dy}{\mathrm dx} = \frac {\mathrm dy} {\mathrm du} \cdot\frac {\mathrm du}{\mathrm dx}

Esta regla es fundamental para entender cómo se relacionan los cambios en diferentes partes de un problema matemático.

Contenido

¿Cómo se escribe la regla de la cadena?
- Notación de Lagrange
- Notación de Leibniz
¿Cuándo se aplica la regla de la cadena?
- Funciones de un solo valor
Ejemplos de la regla de la cadena
Galería de imágenes
Véase también

¿Cómo se escribe la regla de la cadena?

Existen varias maneras de escribir la regla de la cadena, pero todas significan lo mismo. Aquí te mostramos las más comunes:

Notación de Lagrange

Si tenemos dos funciones, digamos f y g, y ambas se pueden "derivar" (es decir, podemos encontrar su tasa de cambio), entonces la regla de la cadena nos dice cómo derivar una función que es la "composición" de ambas. Una función compuesta es cuando aplicas una función y luego otra. Por ejemplo, si h(x) = f(g(x)), significa que primero calculas g(x) y luego aplicas f al resultado.

La fórmula en esta notación es: 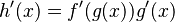$h'(x)=f'(g(x))g'(x)$

Aquí, h'(x) es la derivada de la función compuesta h, f'(g(x)) es la derivada de f evaluada en g(x), y g'(x) es la derivada de g.

Notación de Leibniz

Esta notación es muy útil porque nos ayuda a ver cómo se "cancelan" las variables intermedias. Si una variable z depende de y, y y a su vez depende de x, entonces z también depende de x. La regla de la cadena se escribe así:

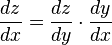
$\frac{dz}{dx}=\frac{dz}{dy}\cdot\frac{dy}{dx}$

Piensa que el dy de arriba y el dy de abajo se "cancelan", dejando dz/dx, que es lo que queremos calcular.

¿Cuándo se aplica la regla de la cadena?

La regla de la cadena se usa cuando una función depende de otra función. Aquí te explicamos el caso más común:

Funciones de un solo valor

Imagina que tienes dos funciones:

Una función g que toma un número de un conjunto I y te da un resultado.
Otra función f que toma un número de un conjunto J y te da un resultado.

Si los resultados de g pueden ser usados como entrada para f (es decir, g(I) está dentro de J), entonces puedes crear una función compuesta f de g (escrita como f ∘ g).

Si g tiene una derivada en un punto a, y f tiene una derivada en el punto g(a), entonces la función compuesta f ∘ g también tiene una derivada en a. La fórmula para calcularla es:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (f \circ g)'(a)=(f'(g(a)))\cdot g'(a)

Si las funciones se pueden derivar en todos sus puntos, podemos escribir la regla de forma más general: 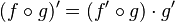$(f\circ g)'=(f'\circ g)\cdot g'$

Para que sea más fácil de leer, a menudo usamos una variable intermedia, por ejemplo, u = g(x). Así, la fórmula se ve como: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac {\text{d}(f \circ g)}{\text{d}x} = \frac{\text{d}f}{\text{d}u} \cdot \frac {\text{d}u}{\text{d}x}

Si tienes muchas funciones encadenadas, por ejemplo, f1 que depende de f2, f2 de f3, y así hasta fn que depende de x, la regla de la cadena se aplica varias veces: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \begin{align} \frac{df_1}{dx} &=\frac{df_1}{df_2}\cdot\frac{df_2}{df_3}\cdot\cdots\cdot\frac{df_n}{dx} \end{align}

Ejemplos de la regla de la cadena

Regla del cociente

La regla de la cadena nos ayuda a entender otras reglas de derivación. Por ejemplo, la Regla del cociente (que se usa para derivar divisiones de funciones) se puede obtener usando la regla de la cadena junto con la regla del producto.

Si queremos derivar una función que es una división, como 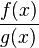$\frac{f(x)}{g(x)}$ , podemos reescribirla como un producto: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f(x) \cdot \frac{1}{g(x)} .

Primero, aplicamos la regla del producto: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \begin{align} \frac{d}{dx}\left(\frac{f(x)}{g(x)}\right) &=f'(x)\cdot\frac{1}{g(x)}+f(x)\cdot\frac{d}{dx}\left(\frac{1}{g(x)}\right) \end{align}

Ahora, para derivar Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{1}{g(x)} , usamos la regla de la cadena. Pensamos en Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{1}{g(x)} como una función compuesta donde la función de afuera es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{1}{u} y la de adentro es 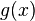$g(x)$ . La derivada de Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{1}{u} es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): -\frac{1}{u^2} .

Aplicando la regla de la cadena: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{d}{dx}\left(\frac{1}{g(x)}\right) = -\frac{1}{g(x)^2} \cdot g'(x)

Sustituyendo esto en la ecuación anterior, obtenemos la regla del cociente: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \begin{align} \frac{d}{dx}\left(\frac{f(x)}{g(x)}\right) &=\frac{f'(x)g(x)-f(x)g'(x)}{g(x)^2} \end{align}

Derivada de funciones inversas

La regla de la cadena también nos permite encontrar la derivada de una función inversa. Si tienes una función g que es derivable y tiene una función inversa f, entonces sabemos que:

$f(g(x))=x$

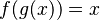
Si derivamos ambos lados de esta ecuación usando la regla de la cadena en el lado izquierdo, obtenemos: 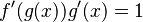$f'(g(x))g'(x)=1$

Para encontrar la derivada de la función inversa f'(y), podemos despejarla: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f'(y)=\frac{1}{g'(f(y))}

Por ejemplo, si 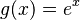$g(x)=e^x$ (la función exponencial), su derivada es 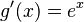$g'(x)=e^x$ . Su función inversa es 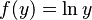$f(y)=\ln y$ (el logaritmo natural). Usando la fórmula, la derivada de Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \ln y es: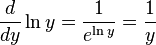 $\frac{d}{dy}\ln y=\frac{1}{e^{\ln y}}=\frac{1}{y}$

Ejemplo conceptual

Imagina que estás subiendo una montaña a una velocidad de 0.5 kilómetros por hora. Sabes que la temperatura baja 6 grados Fahrenheit por cada kilómetro que subes (hace más frío a mayor altura).

Si quieres saber qué tan rápido está cambiando la temperatura con respecto al tiempo, puedes usar la regla de la cadena:

Tasa de cambio de temperatura con respecto a la distancia: 6 °F por kilómetro.
Tasa de cambio de la distancia con respecto al tiempo: 0.5 kilómetros por hora.

Multiplicando estas dos tasas: 6 °F/kilómetro * 0.5 kilómetros/hora = 3 °F/hora

Esto significa que la temperatura está bajando 3 grados Fahrenheit cada hora que subes. Este es un ejemplo práctico de cómo funciona la regla de la cadena.

Ejemplo algebraico

Vamos a calcular la derivada de una función compuesta usando la regla de la cadena. Supongamos que tenemos las funciones:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): y(u)=\ln(u) (el logaritmo natural de u)
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): u(x)=\cos(x) (el coseno de x)

Queremos calcular 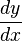$\frac{dy}{dx}$ , es decir, cómo cambia y con respecto a x.

Primero, calculamos las derivadas de cada función por separado:

La derivada de Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): y(u)=\ln(u) con respecto a u es: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{dy}{du}=\frac{1}{u}
La derivada de Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): u(x)=\cos(x) con respecto a x es: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{du}{dx}=-\sen(x)

Ahora, aplicamos la regla de la cadena: 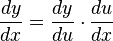$\frac{dy}{dx}=\frac{dy}{du}\cdot\frac{du}{dx}$

Sustituimos las derivadas que calculamos: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \begin{align} \frac{dy}{dx} &=\frac{1}{u}\cdot(-\sen x) \\ &=-\frac{\sen x}{u} \end{align}

Finalmente, reemplazamos u con su valor original en términos de x, que es 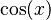$\cos(x)$ : Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \begin{align} \frac{dy}{dx} &=-\frac{\sen x}{\cos x} \\ &=-\tan{x} \end{align}

Este resultado es válido para los valores de x donde 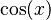$\cos(x)$ es positivo, ya que el logaritmo natural solo se define para números positivos.

Galería de imágenes

Véase también

En inglés: Chain rule Facts for Kids

Derivada
Derivada de la función inversa
Regla del producto
Regla del cociente

Obtenido de «https://ninos.kiddle.co/index.php?title=Regla_de_la_cadena&oldid=4920579»

Todo el contenido de los artículos de la Enciclopedia Kiddle (incluidas las imágenes) se puede utilizar libremente para fines personales y educativos bajo la licencia Atribución-CompartirIgual a menos que se indique lo contrario. Citar este artículo:

Regla de la cadena para Niños. Enciclopedia Kiddle.