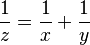Nomograma para niños
Un nomograma es como una calculadora visual. Es un dibujo especial, generalmente en dos dimensiones, que te ayuda a hacer cálculos de forma gráfica y rápida, aunque no siempre con total exactitud. Imagina que es una herramienta que te permite resolver problemas matemáticos complejos usando líneas y puntos en lugar de números en una calculadora.
Los nomogramas son un tipo de herramienta de cálculo analógico, similar a una regla de cálculo. Esto significa que usan longitudes de líneas para representar números. Por eso, su precisión es limitada; depende de lo bien que estén dibujadas las escalas y de lo preciso que seas al leerlas. Los nomogramas eran muy útiles cuando se necesitaban respuestas rápidas y aproximadas, por ejemplo, en trabajos de ingeniería en el campo o para cálculos que se repetían mucho con pequeños cambios.
Contenido
Historia de los Nomogramas
Orígenes de las Herramientas de Cálculo Visual
Desde hace mucho tiempo, las personas han buscado formas de hacer cálculos más fáciles. Instrumentos antiguos como los astrolabios y los cuadrantes, usados en la Edad Media y el Renacimiento, ya ayudaban a resolver problemas matemáticos de forma gráfica.
Un gran avance llegó en el siglo XVII con la invención de la escala de Gunter, que fue la primera vez que una función se representó con una escala graduada. Luego, Descartes inventó la geometría analítica, que permitió dibujar cualquier función matemática como una curva.
Desarrollo de los Nomogramas Modernos
Los ingenieros militares y otros profesionales que hacían muchos cálculos repetitivos fueron los más interesados en estas herramientas. En 1797, L. Pouchet publicó un trabajo que incluía un primer intento de crear tablas gráficas.
Más tarde, en 1842, Léon Lalanne propuso usar estos gráficos para calcular movimientos de tierra. En 1843, formuló un principio llamado anamorfosis, que hizo más fácil dibujar estos gráficos, convirtiendo muchas líneas curvas en rectas. Él los llamó ábacos.
Finalmente, Maurice d'Ocagne en 1884 simplificó aún más las cosas, reemplazando las cuadrículas por escalas graduadas simples. Él llamó a este nuevo campo la nomografía.
El Auge y la Caída de los Nomogramas
Los nomogramas fueron muy populares durante gran parte del siglo XX, especialmente en campos como la ingeniería civil, ingeniería química, ingeniería eléctrica, ingeniería electrónica e ingeniería aeronáutica. Se incluían en manuales y se publicaban colecciones enteras de ellos. Sin embargo, su precisión limitada (solo dos o tres cifras significativas) hacía que no fueran adecuados para campos donde la exactitud es crucial, como la astronomía o las finanzas.
Con la llegada de las calculadoras y los ordenadores electrónicos a finales del siglo XX, los nomogramas dejaron de usarse tanto. Las máquinas podían hacer cálculos exactos mucho más rápido. Aun así, los nomogramas todavía tienen ventajas: permiten ver de un vistazo todas las posibles soluciones de un problema y cómo se relacionan las diferentes partes de una ecuación.
Nomogramas y Tablas
Los nomogramas están relacionados con las tablas de cálculo, que también se usan para resolver problemas y presentar información.
Un ingeniero español, Ricardo Seco, explicó en 1911 que sería ideal tener un libro con todas las tablas posibles para las fórmulas más usadas. Pero esto es casi imposible porque ocuparían mucho espacio y serían muy difíciles de crear, especialmente si una fórmula tiene más de tres variables. Los nomogramas, en cambio, pueden manejar casi cualquier número de variables.
D'Ocagne decía que los nomogramas son como "tablas de cálculos completas". Una ventaja es que puedes "interpolar" visualmente, es decir, estimar valores intermedios. La desventaja es que las tablas pueden ser tan precisas como quieras, mientras que los nomogramas tienen una precisión limitada.
Cómo se Usan los Nomogramas
Un nomograma es la representación gráfica de una ecuación con varias variables. Por lo tanto, tendrá tantos elementos gráficos (puntos o líneas) como variables tenga la ecuación. Si conoces los valores de todas las variables menos una, puedes encontrar el valor de la que falta usando una regla o trazando una línea.
Por ejemplo, un nomograma para una ecuación con dos variables (como y = f(x)) tendrá dos escalas graduadas. Si conoces el valor de una variable, lo marcas en su escala y eso te indicará el valor de la otra variable en su escala. Si la ecuación tiene tres variables (como z = f(x, y)), el nomograma normalmente tendrá tres escalas.
El "arte" de la nomografía es diseñar estas escalas y colocarlas de tal manera que al trazar líneas rectas que las crucen, se encuentren los puntos que representan los valores relacionados por la ecuación.
La forma en que se colocan las escalas depende del problema. Por ejemplo, para convertir grados Celsius a Fahrenheit, un nomograma podría tener dos escalas paralelas. Solo tendrías que poner una regla perpendicular a la escala de la temperatura que conoces, y la regla te mostrará la temperatura equivalente en la otra escala.
Ejemplos de Nomogramas
- La espiral de Cornu, que es un nomograma en forma de espiral.
- La carta de Smith, que se usa en electrónica para entender cómo se comportan las señales.
- El papel milimetrado especial (semilogarítmico, doblemente logarítmico, probabilístico) que permite representar funciones no lineales como líneas rectas.
Un Gráfico Útil para Cálculos
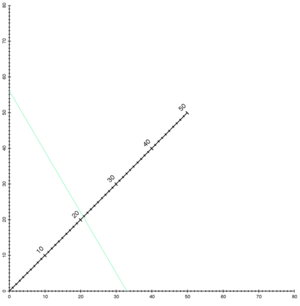
El nomograma de la imagen de arriba ayuda a resolver una ecuación con tres variables:
Esta fórmula se usa para calcular la resistencia total de dos resistores conectados en paralelo, o para saber dónde se forma la imagen de un objeto con una lente delgada en óptica. Lo interesante es que este nomograma hace un cálculo complejo usando solo escalas rectas.
Para usarlo, marcas los valores de x y y en los ejes horizontal y vertical. Luego, unes esos dos puntos con una línea recta. El valor de z se encuentra en la escala diagonal, donde la línea recta la cruza.
En el ejemplo de la imagen, la línea verde muestra que dos resistores de 56 y 33 Ω en paralelo tienen una resistencia total de aproximadamente 21 Ω. O, si un objeto está a 56 cm de una lente con una distancia focal de 21 cm, su imagen se forma a 33 cm de la lente.
Prueba de Chi-cuadrado
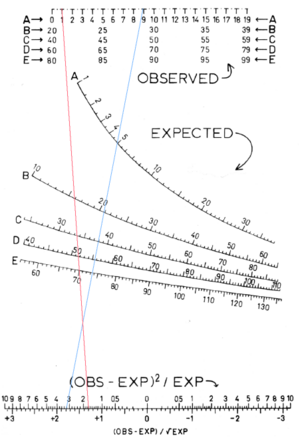
Este nomograma se puede usar para hacer cálculos aproximados para una prueba estadística llamada prueba χ² de Pearson. Este nomograma usa escalas curvas con graduaciones que no están espaciadas de manera uniforme.
La línea azul en el nomograma muestra el cálculo de:
- (9 − 5)2/ 5 = 3,2
Y la línea roja calcula:
- (81 − 70)2 / 70 = 1,7
Ver también
- Escala transversal
- Baremo
Véase también
 En inglés: Nomogram Facts for Kids
En inglés: Nomogram Facts for Kids