Estereorradián para niños
El estereorradián (símbolo: sr) es una unidad especial que usamos para medir los ángulos en tres dimensiones, como si fuera un "trozo" de espacio. Imagina que tienes una esfera y quieres saber cuánto espacio ocupa una parte de ella desde el centro. El estereorradián es el equivalente tridimensional del radián, que mide ángulos en dos dimensiones (como un trozo de pizza en un círculo).
El estereorradián es una unidad que no tiene dimensiones físicas, es decir, no se mide en metros, segundos o kilogramos. Se calcula dividiendo el área de una superficie por el cuadrado de la distancia desde el centro. Aunque no tiene dimensiones, usamos el símbolo "sr" para distinguirlo de otras cantidades sin dimensiones. Por ejemplo, la intensidad de la luz se puede medir en vatios por estereorradián (W⋅sr−1). Antes, el estereorradián era una unidad "suplementaria" en el Sistema Internacional de Unidades (SI), pero desde 1995 se considera una unidad derivada del SI.
Esta unidad es muy importante para entender cómo se distribuyen cosas en el espacio, como la luz, el sonido o incluso cómo vemos las cosas. Se usa en muchos campos de la ciencia, como la astronomía, la medición de la luz (radiometría), la geodesia (medición de la Tierra), los gráficos de computadora y la acústica. Con el estereorradián, podemos hacer mediciones más exactas y mejorar la tecnología y la investigación.
Contenido
¿Qué es un Estereorradián?
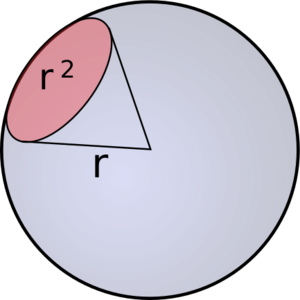
Un estereorradián se define usando una esfera imaginaria con un radio de 1 metro. Si tomas una parte de la superficie de esa esfera que mide 1 metro cuadrado, el ángulo que se forma desde el centro de la esfera hasta los bordes de esa parte es un estereorradián.
Entendiendo la definición del Estereorradián
Para calcular un ángulo sólido en estereorradianes, usamos una fórmula sencilla:
El ángulo sólido (que se representa con la letra griega Omega, Ω) es igual a la superficie (S) que cubre un objeto en una esfera imaginaria, dividida por el radio (r) de esa esfera al cuadrado. El centro de la esfera debe coincidir con el punto desde donde se mide el ángulo.
Así, un estereorradián es el ángulo que cubre una superficie que tiene el mismo tamaño que el cuadrado del radio, a una distancia igual al radio desde el centro.
- Analogía con el radián:
Imagina un círculo en dos dimensiones. El radián mide un ángulo en un círculo. Se calcula dividiendo la longitud de un arco (una parte de la circunferencia) por el radio del círculo. El estereorradián es similar, pero en tres dimensiones, usando una superficie en lugar de una longitud de arco.
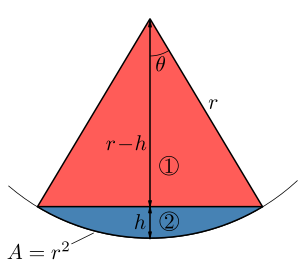
Ángulo de un Cono Esférico
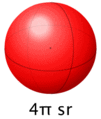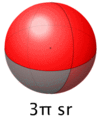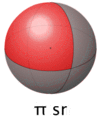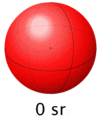
Si el área que estamos midiendo es la de un "casquete esférico" (como la parte superior de una pelota cortada), y esa área es igual al radio al cuadrado, entonces el ángulo sólido que forma el cono que va desde el centro hasta ese casquete se puede calcular.
Otras Características del Estereorradián
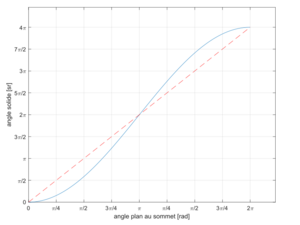
Un estereorradián también se puede entender como el ángulo que forma un cono con una apertura de aproximadamente 65.54 grados. Si giras un ángulo plano de 65.54 grados alrededor de su centro, se forma un cono que abarca un ángulo sólido de 1 estereorradián.
Un estereorradián también representa una parte muy pequeña de una esfera completa, aproximadamente 1/4π de una esfera.
Múltiplos en el Sistema Internacional
En el Sistema Internacional de Unidades, a veces se usan unidades más pequeñas para el estereorradián, como el miliestereorradián (msr) y el microestereorradián (μsr). Estas se usan para describir haces de luz o partículas muy finos. Otros múltiplos más grandes casi no se usan.
¿Para qué se Usa el Estereorradián?
El estereorradián se usa mucho en radiometría y fotometría, que son las ciencias que miden la luz y otras formas de radiación. Por ejemplo, la intensidad de la luz que emite una fuente se mide en vatios por estereorradián. Esto nos ayuda a saber cuánta energía de luz se envía en una dirección específica.
Ejemplos Prácticos
- La vista de un ojo humano puede abarcar un ángulo sólido de aproximadamente 2π estereorradianes.
- Imagina un cono. El ángulo sólido que forma ese cono se puede calcular usando el ángulo de su punta. Por ejemplo, si un cono tiene un ángulo de apertura de 65.54 grados, el espacio que abarca es de 1 estereorradián.
Fórmulas de la Luz y el Estereorradián
El lumen es la unidad que mide la cantidad total de luz visible que emite una fuente. Un lumen es la luz que emite una fuente con una intensidad luminosa de 1 candela dentro de un ángulo sólido de 1 estereorradián.
Aquí te mostramos cómo se relacionan estas unidades:
- 1 lumen (lm) = 1 candela (cd) × 1 estereorradián (sr)
- 1 lux (lx) = (1 candela (cd) × 1 estereorradián (sr)) / 1 metro cuadrado (m²)
Donde:
- lm: es el lumen, la unidad de flujo luminoso.
- sr: es el estereorradián, la unidad de ángulo sólido.
- cd: es la candela, la unidad de intensidad luminosa.
- lx: es el lux, la unidad de iluminancia (cuánta luz llega a una superficie).
Usos Importantes del Estereorradián
Astronomía y Astrofísica
En astronomía, el estereorradián se usa para medir el tamaño aparente de los objetos celestes desde la Tierra. Por ejemplo, los astrónomos pueden calcular cuánto espacio en el cielo ocupa la Luna o una estrella usando estereorradianes. Esto les ayuda a entender la intensidad de la luz o la radiación que viene de esos objetos.
Radiometría y Fotometría
En la radiometría, que mide la radiación óptica (incluyendo la luz), los estereorradianes son clave para saber cuánta luz o energía emite una fuente en una dirección específica. Esto es muy útil para caracterizar fuentes de luz como los láseres o las bombillas.
Geodesia y Cartografía
En geodesia, que es la ciencia que mide y representa la superficie de la Tierra, el estereorradián se usa para calcular áreas en la superficie curva de nuestro planeta. Esto es fundamental para la navegación y para hacer mapas precisos, especialmente cuando se trabaja con proyecciones que tienen en cuenta la forma esférica de la Tierra.
Gráficos por Computadora y Visión
En los gráficos por computadora y la visión artificial, los estereorradianes se usan para simular cómo ven las cámaras reales y virtuales. El "campo de visión" de una cámara en un videojuego o en un programa de diseño 3D se puede expresar en estereorradianes para saber cuánto de la escena virtual es visible. Esto es muy importante en la realidad virtual y la realidad aumentada para que los usuarios perciban los entornos 3D de forma realista.
Acústica y Medición del Sonido
Los estereorradianes también se usan en la acústica para medir la intensidad y cómo se distribuye el sonido en el espacio. Las fuentes de sonido, como los altavoces, pueden describirse por el ángulo sólido que cubren. Esto permite modelar con más precisión cómo se propaga el sonido, lo cual es útil en la acústica de edificios y en la ingeniería de audio.
Galería de imágenes
Véase también
 En inglés: Steradian Facts for Kids
En inglés: Steradian Facts for Kids
- Ángulo sólido
- Radian
- Unidades básicas del Sistema Internacional
- Unidades derivadas del Sistema Internacional
- Grado cuadrado
- Ley de Lambert