Proyección de Robinson para niños
La proyección de Robinson es una forma especial de dibujar el mapamundi en una superficie plana. Imagina que tienes una pelota de baloncesto y quieres dibujarla en una hoja de papel sin que se rompa ni se estire demasiado. ¡Es un desafío! Esta proyección fue creada para resolver ese problema, buscando la mejor manera de mostrar todo el mundo de forma que se vea bien y sea fácil de entender.
Fue diseñada por Arthur H. Robinson en 1961. Durante un tiempo, fue muy popular y la usaron empresas importantes como Rand McNally (que hace mapas) y la National Geographic Society (conocida por sus revistas y documentales sobre geografía). Más tarde, la National Geographic Society cambió a otra proyección llamada proyección de Winkel-Tripel.
Contenido
¿Qué hace especial a la proyección de Robinson?
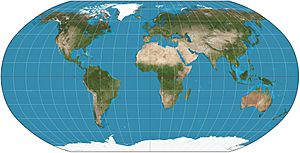
¿Cómo se ve el mundo en un mapa de Robinson?
La proyección de Robinson es un tipo de mapa que busca un equilibrio. No es un mapa que mantenga las áreas de los países exactamente iguales a como son en la realidad (no es "equiárea"), ni tampoco mantiene las formas perfectas de los continentes (no es "conforme"). En cambio, su creador pensó que era mejor sacrificar un poco de ambas cosas para lograr un mapa que se viera bien en general.
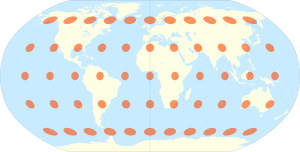
En este mapa, las líneas que van de norte a sur (los meridianos) se curvan suavemente, lo que ayuda a que el mapa no se vea demasiado estirado. Sin embargo, los polos (el Polo Norte y el Polo Sur) no aparecen como puntos, sino como líneas largas. Esto significa que las zonas cercanas a los polos se ven un poco estiradas o distorsionadas.
¿Dónde se nota la distorsión en el mapa de Robinson?
La distorsión es más notable cerca de los polos, donde las formas y los tamaños no son tan precisos. Pero a medida que te alejas de los polos y te acercas al centro del mapa, la distorsión disminuye y el mapa se ve bastante bien. Las líneas que van de este a oeste (los paralelos) son rectas, lo que puede causar que las formas se vean un poco raras en las zonas más al norte o al sur, cerca de los bordes del mapa. A pesar de esto, cuando se creó, la proyección de Robinson logró su objetivo de crear mapas del mundo que fueran atractivos y fáciles de usar.
Galería de imágenes
Véase también
 En inglés: Robinson projection Facts for Kids
En inglés: Robinson projection Facts for Kids