Problema del final feliz para niños
El "problema del final feliz" es un desafío matemático muy interesante. Fue nombrado así por el famoso matemático Paul Erdős porque su descubrimiento llevó al matrimonio de George Szekeres y Esther Klein.
Este problema plantea lo siguiente: si tienes cinco puntos en un plano (como una hoja de papel), y ninguno de esos puntos está en línea recta con otros dos (a esto se le llama "posición general"), siempre podrás encontrar cuatro de esos puntos que formen un cuadrilátero convexo. Un cuadrilátero convexo es una figura de cuatro lados donde todos sus ángulos "apuntan hacia afuera", es decir, no tiene ninguna "curva hacia adentro". Imagina un cuadrado o un rectángulo; esos son cuadriláteros convexos.
Este problema fue uno de los primeros descubrimientos que ayudaron a desarrollar una parte de las matemáticas llamada teoría de Ramsey, que estudia cómo el orden aparece en sistemas grandes.
Contenido
¿Cómo se demuestra el problema del final feliz?
La idea principal para demostrar este teorema es analizar diferentes situaciones.
- Si cuatro o más de los puntos están en el borde exterior de la figura que forman (lo que se llama la "envolvente convexa"), entonces puedes elegir esos cuatro puntos para formar el cuadrilátero convexo.
- Si, por otro lado, los puntos forman una especie de triángulo grande con dos puntos dentro, puedes elegir los dos puntos de adentro y dos de los puntos del triángulo grande para formar el cuadrilátero convexo.
La Conjetura de Erdős-Szekeres
La conjetura de Erdős-Szekeres es una idea más general que relaciona cuántos puntos necesitas para asegurar que siempre habrá un polígono convexo de un cierto número de lados. Se cree que el número más pequeño de puntos en posición general para que siempre contengan un polígono convexo de N lados es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 2^{N-2}+1 . Esta conjetura aún no se ha demostrado por completo, pero los matemáticos han encontrado algunas pistas.
Polígonos convexos más grandes
Los matemáticos Erdős y Szekeres demostraron una idea más grande:
- Para cualquier número de lados N que quieras, si tienes un grupo de puntos lo suficientemente grande en posición general, siempre podrás encontrar N puntos que formen un polígono convexo.
Esta demostración apareció en el mismo estudio donde probaron otro teorema importante sobre secuencias de números.
Los matemáticos usan la letra f ( N ) para representar el número mínimo de puntos que necesitas para garantizar que siempre encontrarás un polígono convexo de N lados. Se sabe que:
- f (3) = 3: Con 3 puntos, siempre puedes formar un triángulo (que es un polígono convexo de 3 lados).
- f (4) = 5: Con 5 puntos, siempre puedes formar un cuadrilátero convexo (como vimos en el problema del final feliz).
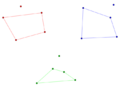
- f (5) = 9: Necesitas al menos 9 puntos para asegurar que siempre habrá un pentágono convexo (una figura de 5 lados). La imagen muestra un ejemplo de 8 puntos donde no hay un pentágono convexo.
- f (6) = 17: Necesitas al menos 17 puntos para asegurar que siempre habrá un hexágono convexo (una figura de 6 lados).
- Para N mayor que 6, el valor exacto de f ( N ) aún no se conoce, pero se sabe que siempre es un número finito.
Basándose en los valores conocidos, Erdős y Szekeres propusieron una fórmula en su trabajo original: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f(N) = 1 + 2^{N-2} para cualquier N igual o mayor que 3. Más tarde, demostraron que el número de puntos necesarios es al menos Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 1 + 2^{N-2} .
Polígonos convexos "vacíos"
También existe una pregunta sobre los polígonos convexos "vacíos". Un polígono convexo es "vacío" si no tiene ningún otro punto del conjunto original en su interior.
- Se sabe que cinco puntos en posición general siempre contienen un cuadrilátero convexo vacío.
- Diez puntos en posición general siempre tienen un pentágono convexo vacío.
- Sin embargo, existen grupos de puntos muy grandes que no contienen un heptágono (7 lados) convexo vacío.
Durante mucho tiempo, los matemáticos se preguntaron si siempre existirían hexágonos (6 lados) convexos vacíos. Finalmente, en 2007 y 2008, dos matemáticos, Nicolás y Gerken, demostraron que sí, que cualquier grupo de puntos lo suficientemente grande en posición general siempre contiene un hexágono convexo vacío. Se ha demostrado que se necesitan al menos 30 puntos para garantizar un hexágono convexo vacío.
Galería de imágenes
-
El problema del final feliz: cada conjunto de cinco puntos en posición general contiene los vértices de un cuadrilátero convexo
Véase también
En inglés: Happy ending problem Facts for Kids
