Paradoja de la línea de costa para niños
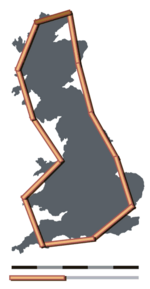
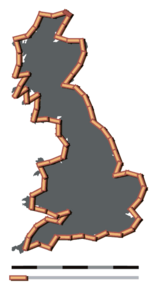
La paradoja de la línea de costa es una idea sorprendente que explica por qué es imposible medir con exactitud la longitud de la costa de cualquier masa de tierra. Esto sucede porque las líneas costeras tienen una naturaleza similar a los fractales. Cuanto más de cerca miras una costa, más detalles y curvas encuentras.
Esta observación fue notada por primera vez por el científico Lewis Fry Richardson. Más tarde, el matemático Benoît Mandelbrot desarrolló esta idea. Él demostró que la longitud que se obtiene al medir una costa siempre depende de la herramienta o la escala que uses.
Contenido
Paradoja de la línea de costa: ¿Por qué es difícil medirla?
La longitud de una línea de costa cambia según el método que uses para medirla. Una costa tiene detalles de todos los tamaños. Estos van desde grandes bahías de cientos de kilómetros hasta pequeñas rocas y granos de arena.
Como no hay un tamaño mínimo obvio para medir, no podemos fijar una única longitud definitiva para la costa. Solo podemos obtener diferentes estimaciones. Estas estimaciones dependen de la medida mínima que decidamos considerar.
La Geometría y la Medición de Curvas
El concepto de longitud viene de la geometría clásica. En esta geometría, una línea recta es la distancia más corta entre dos puntos. Esta línea tiene una longitud única y bien definida.
Medir la longitud de una curva geométrica es más complejo. Si la curva es "suave" (sin cambios bruscos), podemos aproximar su longitud. Hacemos esto sumando la medida de muchos segmentos rectos muy pequeños que conectan los puntos de la curva.
Si usamos pocos segmentos, la estimación será baja. Si usamos segmentos cada vez más cortos, la suma se acercará a la longitud real de la curva. Para encontrar el valor exacto, los matemáticos usan el cálculo. Esta rama de las matemáticas trabaja con cantidades infinitamente pequeñas.
¿Qué son las Curvas Fractales?
No todas las curvas se pueden medir de esta manera. Un fractal es una curva cuya complejidad no disminuye, incluso si aumentas la escala de observación.
Mientras que las mediciones de una curva suave se acercan a un solo valor, las mediciones de una curva fractal siguen cambiando. Esto ocurre porque siempre aparecen nuevos detalles al mirar más de cerca.
La longitud de un fractal matemático "perfecto" siempre tiende a ser infinita. Si intentáramos medir una línea costera con una resolución infinita, la longitud acumulada de todos los pliegues y detalles infinitamente pequeños crecería sin parar.
Líneas Costeras Reales y la Escala de Medición
Las líneas costeras son objetos físicos y no son fractales matemáticos perfectos. Los detalles muy pequeños (de 1 centímetro o menos) cambian constantemente debido a la erosión y la dinámica del mar. Por lo tanto, el concepto de un fractal infinito no se aplica estrictamente a una costa real.
En la práctica, debemos elegir una escala de medición adecuada. Si medimos una costa en kilómetros, ignoramos las variaciones mucho menores a un kilómetro. Si la medimos en centímetros, debemos incluir todos los pequeños detalles de ese tamaño.
Es importante establecer criterios claros para definir la línea de costa. Esto es especialmente cierto en lugares como estuarios o llanuras de marea. Usar diferentes métodos para diferentes unidades de medida hace que sea difícil convertir las longitudes entre sí.
Ejemplos de Costas Extremadamente Irregulares
Algunos ejemplos extremos de esta paradoja se ven en las costas muy accidentadas. Esto incluye lugares como Noruega, Chile y la costa del Noroeste del Pacífico en América del Norte.
Por ejemplo, la costa de la Columbia Británica en Canadá es muy compleja. A lo largo de solo 965 kilómetros en línea recta, sus curvas e islas añaden una longitud enorme. Esta sección representa más del 10% de la longitud total de la costa de Canadá.
Conceptos relacionados con la Paradoja
- Costa
- Dimensión Fractal: Una forma de medir cuán "áspero" o complejo es un objeto fractal.
- Cuerno de Gabriel: Una figura geométrica curiosa que tiene una superficie infinita, pero un volumen finito.
- Paradoja sorites: Una paradoja que trata sobre cómo los pequeños cambios graduales pueden llevar a un resultado ambiguo.
Galería de imágenes
-
Animación que muestra cómo se puede determinar con precisión la longitud de una curva suave usando segmentos cada vez más pequeños.
Véase también
En inglés: Coastline paradox Facts for Kids
