Optimización (matemática) para niños
En matemáticas, estadística, economía y ciencia de la computación, la optimización es el proceso de elegir el mejor elemento de un grupo de opciones disponibles. Imagina que tienes varias maneras de hacer algo; la optimización te ayuda a encontrar la que funciona mejor según lo que necesites.
En su forma más sencilla, un problema de optimización busca el valor más alto (maximizar) o el más bajo (minimizar) de una función. Para lograrlo, se prueban diferentes valores de entrada y se calcula el resultado. La optimización es una parte muy importante de las matemáticas aplicadas y se usa para encontrar las "mejores soluciones" en muchos campos.
Optimizar significa hacer algo de la manera más eficiente posible. Esto a menudo implica usar la menor cantidad de recursos, como tiempo o dinero, para obtener el mejor resultado. Aunque el término se usa mucho en informática, también es fundamental en matemáticas, gestión de proyectos y economía.
Contenido
Problemas de Optimización: ¿Cómo se Plantean?
Un problema de optimización se puede describir así:
- Tenemos una función (como una fórmula matemática) que queremos analizar.
- Buscamos un valor específico que haga que esa función sea lo más pequeña posible (minimizar) o lo más grande posible (maximizar).
Este tipo de problema se llama problema de optimización o problema de programación matemática. El término "programación" aquí no se refiere a la programación de computadoras, sino a la planificación de actividades. Muchos desafíos del mundo real se pueden resolver usando este método. Por ejemplo, en física, se usa para encontrar el estado de menor energía de un sistema.
El conjunto de todos los valores posibles que podemos elegir se llama espacio de búsqueda o conjunto de elección. Los valores que cumplen con todas las condiciones se llaman soluciones candidatas o soluciones factibles.
La función que queremos maximizar o minimizar se llama función objetivo. Una solución que logra el mejor valor para esta función (el más bajo o el más alto) se llama solución óptima.
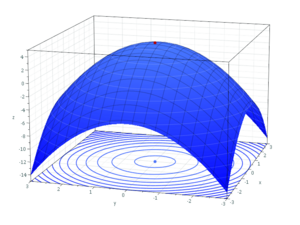
Por lo general, los problemas de optimización se plantean como problemas de minimización. Si una función no es "convexa" (una forma matemática específica), puede tener varios puntos donde alcanza un mínimo local. Un mínimo local es el punto más bajo en una pequeña área, pero no necesariamente el más bajo de toda la función. Encontrar el mínimo global (el más bajo de todos) en problemas complejos es el objetivo de la optimización global.
Notación en Optimización
Los problemas de optimización a menudo se escriben con símbolos especiales.
Valor Mínimo y Máximo de una Función
Cuando ves esto: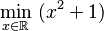 
Significa que queremos encontrar el valor más pequeño de la función 
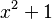, donde x puede ser cualquier número real. El valor más pequeño es 1, y se logra cuando x es 0.
De manera similar, esto: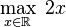 
Pide el valor más grande de la función 2x, donde x es cualquier número real. En este caso, no hay un valor máximo definido, porque 2x puede crecer infinitamente.
Argumentos de la Entrada Óptima
La siguiente expresión:
![\underset{x\in(-\infty,-1]}{\operatorname{arg\,min}} \; x^2 + 1,](/images/math/f/3/5/f356685bbb0bdac5fbffe93dc801f459.png)
o
![\underset{x}{\operatorname{arg\,min}} \; x^2 + 1, \; \text{sujeto a:} \; x\in(-\infty,-1].](/images/math/4/a/0/4a06632441c4a5ce5def94bfc768db25.png)
Busca el valor de x en el intervalo ![(-\infty,-1]](/images/math/2/b/b/2bbda46f09c030f245f9afe1fa0eb85f.png)
que hace que la función x2 + 1 sea lo más pequeña posible. La respuesta es x = -1, porque 0 no está en el intervalo permitido.
Las expresiones arg min y arg max significan "argumento del mínimo" y "argumento del máximo". Se refieren al valor de la entrada que produce el resultado óptimo, no al resultado óptimo en sí.
Historia de la Optimización
Grandes matemáticos como Pierre de Fermat y Joseph Louis Lagrange desarrollaron fórmulas usando el cálculo para encontrar los valores óptimos. Otros, como Isaac Newton y Carl Friedrich Gauss, crearon métodos para acercarse a la solución óptima paso a paso.
El término "programación lineal" para ciertos problemas de optimización fue popularizado por George B. Dantzig. Él publicó el Algoritmo símplex en 1947, una herramienta muy importante para resolver estos problemas. El término "programación" en este contexto viene del uso militar de "programa" para referirse a planes y logística.
Otros investigadores importantes en este campo incluyen a:
- Richard Bellman
- Narendra Karmarkar
- Leonid Kantorovich
- John von Neumann
Tipos de Optimización
La optimización se divide en varios subcampos, cada uno para diferentes tipos de problemas.
Optimización Lineal y Convexa
- Programación lineal (PL): Aquí, la función que queremos optimizar y las condiciones que deben cumplirse son todas líneas rectas o planos. Es como encontrar el mejor punto dentro de una figura geométrica formada por líneas.
- Programación convexa: Es un caso más general donde la función objetivo tiene una forma "convexa" (como un cuenco hacia arriba si minimizamos) y el área de búsqueda también es convexa. Esto facilita encontrar la solución óptima.
Optimización No Lineal y con Incertidumbre
- Programación no lineal: Este es el caso más general, donde la función objetivo o las condiciones pueden tener formas curvas o más complejas. Puede ser más difícil de resolver que la programación lineal.
- Programación estocástica: Se usa cuando algunos datos del problema son inciertos o dependen del azar.
- Programación robusta: Similar a la estocástica, pero busca soluciones que funcionen bien incluso si hay pequeñas imprecisiones en los datos.
Optimización Combinatoria y Heurísticas
- Optimización combinatoria: Se ocupa de problemas donde las soluciones posibles son un número limitado de opciones discretas, como elegir el mejor camino en una red de ciudades.
- Heurísticas y Metaheurísticas: Son métodos que no garantizan encontrar la solución perfecta, pero son muy útiles para encontrar soluciones "suficientemente buenas" para problemas muy difíciles y grandes. Piensa en ellas como atajos inteligentes.
¿Cómo se Resuelven los Problemas de Optimización?
Para resolver estos problemas, los investigadores usan diferentes técnicas.
Algoritmos y Métodos Iterativos
- Algoritmos: Son pasos definidos que, si se siguen, garantizan una solución en un número finito de pasos. El Algoritmo símplex es un ejemplo famoso para la programación lineal.
- Métodos iterativos: Estos métodos se acercan a la solución óptima paso a paso. Cada paso mejora la solución anterior. Algunos métodos usan información sobre cómo cambia la función (sus "derivadas") para ir más rápido.
* El Método de Newton es un ejemplo que usa información más detallada para converger rápidamente. * El Descenso del gradiente es un método más lento pero útil para problemas muy grandes.
Heurísticas: Soluciones Aproximadas
Cuando un problema es demasiado complejo para los algoritmos exactos, las heurísticas son muy útiles. No siempre encuentran la solución perfecta, pero sí una muy buena. Algunos ejemplos son:
- Algoritmos genéticos: Inspirados en la evolución biológica, prueban muchas soluciones y "mejoran" las mejores con el tiempo.
- Optimización por enjambre de partículas: Se basa en cómo se mueven los grupos de animales (como aves o peces) para encontrar la mejor ubicación.
- Método Nelder-Mead: Una heurística popular que no necesita calcular derivadas.
Clasificación de Puntos Clave
¿Es Posible Resolver el Problema?
La "factibilidad" de un problema se refiere a si existe al menos una solución que cumpla con todas las condiciones. Si no hay ninguna solución posible, el problema es "infactible".
¿Existe una Solución Óptima?
El teorema de Weierstrass nos dice que si una función es continua y el área de búsqueda es "compacta" (cerrada y limitada), entonces siempre habrá un valor máximo y un valor mínimo.
Condiciones para Encontrar el Óptimo
Para encontrar los puntos óptimos, los matemáticos usan herramientas como las derivadas. Un punto donde la primera derivada de la función es cero se llama "punto estacionario" y es un candidato a ser un máximo o un mínimo. Para problemas con restricciones, se usan los multiplicadores de Lagrange y las condiciones de Karush-Kuhn-Tucker.
¿Es un Máximo o un Mínimo?
Una vez que encontramos un punto estacionario, necesitamos saber si es un máximo, un mínimo o un punto de silla (como la parte central de una silla de montar). Para esto, se usa la segunda derivada o una matriz especial llamada matriz Hessiana.
Cuando la función objetivo es "convexa", cualquier mínimo local que encontremos será también el mínimo global, lo que facilita mucho la búsqueda de la mejor solución.
Véase también
En inglés: Mathematical optimization Facts for Kids
