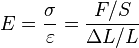Módulo de Young para niños
El módulo de Young (también llamado módulo de elasticidad longitudinal) es una medida que nos dice qué tan rígido o elástico es un material. Imagina que estiras o aprietas algo, como una banda elástica o un trozo de metal. El módulo de Young nos ayuda a entender cuánto se estira o se encoge ese material cuando le aplicamos una fuerza. Es como una "tarjeta de identidad" para cada material que nos indica cómo se comporta bajo presión.
Contenido
¿De dónde viene el nombre?
La palabra "módulo" viene del latín modulus, que significa "medida pequeña". El nombre "módulo de Young" se debe al científico inglés Thomas Young, quien estudió este comportamiento de los materiales en el siglo XIX. Sin embargo, la idea de cómo los materiales se deforman ya había sido explorada antes por otros científicos como Leonhard Euler en 1727 y Giordano Riccati en 1782.
¿Qué nos dice el módulo de Young?
El módulo de Young nos ayuda a saber si un material es muy rígido (como el acero) o más flexible (como la goma).
- Si un material tiene un módulo de Young alto, significa que es muy rígido. Necesitarás mucha fuerza para estirarlo o comprimirlo, y no se deformará mucho. Piensa en una viga de acero.
- Si un material tiene un módulo de Young bajo, significa que es más elástico o flexible. Se estirará o encogerá más fácilmente con menos fuerza. Piensa en una banda de goma.
Este valor es una constante para cada material, siempre y cuando la fuerza que apliquemos no sea tan grande como para deformarlo permanentemente. Si estiras una barra de metal y vuelve a su forma original, el módulo de Young se mantiene. Pero si la estiras tanto que se dobla y no regresa, entonces has superado su límite elástico.
¿Cómo se calcula el módulo de Young?
Para materiales que se comportan de forma lineal (es decir, que se estiran o encogen de manera proporcional a la fuerza aplicada), el módulo de Young se calcula dividiendo la tensión entre la deformación.
- Tensión (σ): Es la fuerza que aplicamos sobre un área específica del material. Se calcula como la fuerza dividida por el área donde se aplica.
- Deformación (ε): Es cuánto se estira o encoge el material en relación con su tamaño original. Se calcula como el cambio de longitud dividido por la longitud inicial.
La fórmula es:
| Símbolo | Nombre |
|---|---|
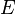 |
Módulo de Young |
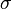 |
Tensión (fuerza por área) |
 |
Deformación (cambio de longitud por longitud inicial) |
Esto significa que si aplicamos la misma fuerza a dos objetos idénticos hechos de materiales diferentes, el que tenga un módulo de Young más alto se deformará menos. ¡Será más difícil de estirar o comprimir!
¿Qué pasa con los materiales que no son lineales?
Algunos materiales, como el cobre, no se estiran o encogen de forma perfectamente lineal. Para ellos, la relación entre la tensión y la deformación no es siempre la misma. En estos casos, se usan otras formas de calcular un módulo de Young "aparente", como el módulo de elasticidad secante o el módulo de elasticidad tangente, que consideran cómo cambia la deformación a medida que aumenta la fuerza.
Unidades de medida
El módulo de Young se mide en unidades de presión, porque es una relación entre fuerza y área. En el Sistema Internacional de Unidades, la unidad más común es el Pascal (Pa).
A menudo, se usan múltiplos del Pascal para que los números sean más fáciles de manejar:
- kPa (kilopascales): Para materiales muy blandos, como algunos tejidos del cuerpo.
- MPa (megapascales): Para materiales como la madera o el hueso.
- GPa (gigapascales): Para materiales muy rígidos, como los metales.
¿Dónde podemos encontrar los valores del módulo de Young?
Existen tablas donde puedes consultar los valores del módulo de Young para muchos materiales diferentes. Esto es muy útil para ingenieros y científicos que necesitan elegir el material adecuado para construir algo, como un puente, un edificio o incluso un juguete.
Galería de imágenes
-
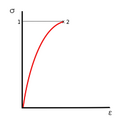
Diagrama tensión - deformación. El módulo de Young se relaciona con la inclinación de la curva. Para materiales como el acero, esta inclinación es casi constante dentro de su límite elástico.
Véase también
 En inglés: Young's modulus Facts for Kids
En inglés: Young's modulus Facts for Kids