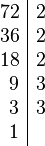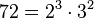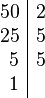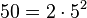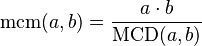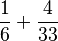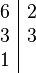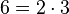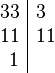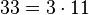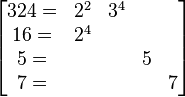robot de la enciclopedia para niños

Mínimo común múltiplo para niños

Enciclopedia para niños
No debe confundirse con Mínimo común denominador o Máximo común divisor.

En matemáticas, el mínimo común múltiplo (mcm o m. c. m.) de dos o más números naturales es el número más pequeño que es múltiplo de todos ellos. Imagina que tienes dos números, como el 2 y el 3. Sus múltiplos son:

  • Múltiplos de 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, ...
  • Múltiplos de 3: 3, 6, 9, 12, 15, 18, ...

Los múltiplos que tienen en común son 6, 12, 18, y así sucesivamente. De todos esos múltiplos comunes, el más pequeño es el 6. Por eso, el mínimo común múltiplo de 2 y 3 es 6. Este concepto es muy útil, especialmente cuando trabajamos con fracciones.

¿Cómo calcular el mínimo común múltiplo (m. c. m.)?

Para encontrar el mcm de dos o más números, podemos usar un método llamado "descomposición en factores primos". Esto significa que vamos a dividir cada número en sus factores primos (números que solo se pueden dividir por 1 y por sí mismos, como 2, 3, 5, 7, etc.).

Descomposición en factores primos

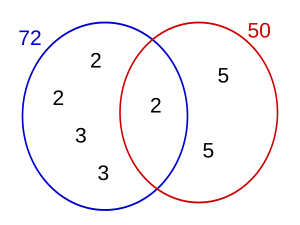
Vamos a calcular el mcm de 72 y 50. Primero, descomponemos cada número en sus factores primos:

Archivo:Divisores 50 72
Descomposición en factores primos de 72 y 50.
\begin{array}{r|l} 72 & 2 \\ 36 & 2 \\ 18 & 2 \\ 9 & 3 \\ 3 & 3 \\ 1 & \end{array}
72 = 2^3 \cdot 3^2 \,
\begin{array}{r|l} 50 & 2 \\ 25 & 5 \\ 5 & 5 \\ 1 & \end{array}
50 = 2 \cdot 5^2 \,

Ahora que tenemos los factores primos de cada número:

  • 72 = 2 x 2 x 2 x 3 x 3 = 2³ x 3²
  • 50 = 2 x 5 x 5 = 2¹ x 5²

Para encontrar el mcm, tomamos todos los factores primos que aparecen en cualquiera de las descomposiciones (en este caso, 2, 3 y 5) y los elevamos a la potencia más alta con la que aparecen.

  • El factor 2 aparece como 2³ (en 72) y 2¹ (en 50). Elegimos la potencia más alta: 2³.
  • El factor 3 aparece como 3² (en 72).
  • El factor 5 aparece como 5² (en 50).

Multiplicamos estos factores con sus potencias más altas:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \operatorname{MCM} (72, 50) = 2^3 \cdot 3^2 \cdot 5^2 = 8 \cdot 9 \cdot 25 = 72 \cdot 25 = 1800

Así, el mcm de 72 y 50 es 1800.

Usando el Máximo Común Divisor (MCD)

También puedes calcular el mcm de dos números si ya conoces su máximo común divisor (MCD). El MCD es el número más grande que divide a ambos números sin dejar resto.

La fórmula es:

\operatorname{mcm}(a, b) = \frac {a \cdot b}{\operatorname{MCD}(a, b)}

Esto significa que el mcm de dos números es igual al producto de esos dos números dividido por su MCD.

Propiedades importantes del mcm

  • Si un número es múltiplo de otro, el mcm de ambos es el número más grande. Por ejemplo, el mcm de 4 y 8 es 8, porque 8 es múltiplo de 4.
  • Si dos números son primos entre sí (es decir, su único divisor común es 1), su mcm es simplemente el resultado de multiplicarlos. Por ejemplo, el mcm de 3 y 5 es 15 (3 x 5).
  • El MCD de varios números siempre es un divisor de su mcm.

Aplicaciones del mínimo común múltiplo (m.c.m)

El mcm es muy útil en varias situaciones matemáticas.

Sumar y restar fracciones

Una de las aplicaciones más comunes del mcm es cuando necesitas sumar o restar fracciones que tienen diferentes denominadores. Para hacer esto, necesitas encontrar un "denominador común", y el más fácil de usar es el mínimo común múltiplo de los denominadores.

Veamos un ejemplo:

\frac {1}{6} + \frac {4}{33}

Para sumar estas fracciones, necesitamos que tengan el mismo denominador. Buscamos el mcm de 6 y 33.

Archivo:Divisores 6 33
Descomposición en factores primos de 6 y 33.
\begin{array}{r|l} 6 & 2 \\ 3 & 3 \\ 1 & \end{array}
6 = 2 \cdot 3 \,
\begin{array}{r|l} 33 & 3 \\ 11 & 11 \\ 1 & \end{array}
33 = 3 \cdot 11 \,
  • 6 = 2 x 3
  • 33 = 3 x 11

El mcm de 6 y 33 es 2 x 3 x 11 = 66.

Ahora, convertimos cada fracción en una fracción equivalente con denominador 66:

  • Para \frac{1}{6}: ¿Por cuánto multiplicamos 6 para obtener 66? Por 11. Entonces, multiplicamos el numerador y el denominador por 11: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{1 \cdot 11}{6 \cdot 11} = \frac{11}{66} .
  • Para Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{4}{33} : ¿Por cuánto multiplicamos 33 para obtener 66? Por 2. Entonces, multiplicamos el numerador y el denominador por 2: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{4 \cdot 2}{33 \cdot 2} = \frac{8}{66} .

Ahora que tienen el mismo denominador, podemos sumarlas:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \cfrac {11}{66} + \cfrac {8}{66} \quad = \quad \cfrac {19}{66}

En expresiones algebraicas

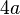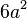El mcm también se usa en expresiones algebraicas para encontrar la expresión más sencilla que es divisible por otras expresiones dadas. Por ejemplo, el mcm de 4a y 6a^2 es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 12a^2 . Esto es importante para simplificar fracciones y resolver ecuaciones en álgebra.

Algoritmo para calcular el mcm de varios números

Si tienes más de dos números, puedes seguir estos pasos:

  1. Descompón cada número en un producto de potencias de sus factores primos. Por ejemplo, 324 es 2² · 3⁴.
  2. De todas las potencias de factores primos que encontraste, elige todos los factores que aparezcan (comunes y no comunes) y, para cada uno, toma la potencia más alta.
  3. Multiplica todos los factores elegidos.

Por ejemplo, calculemos el mcm de 324, 16, 7 y 5:

  • 324 = 2² · 3⁴
  • 16 = 2⁴
  • 7 = 7¹
  • 5 = 5¹
\begin{bmatrix} 324 = & 2^{2} & 3^{4} & & \\ 16 = & 2^{4} & & \\ 5 = & & & 5 & \\ 7 = & & & & 7 \end{bmatrix}

Tomamos las potencias más altas de cada factor primo:

  • Para el factor 2: la potencia más alta es 2⁴ (de 16).
  • Para el factor 3: la potencia más alta es 3⁴ (de 324).
  • Para el factor 5: la potencia más alta es 5¹ (de 5).
  • Para el factor 7: la potencia más alta es 7¹ (de 7).

Multiplicamos estos resultados: 2⁴ · 3⁴ · 5¹ · 7¹ = 16 · 81 · 5 · 7 = 45360. Así, el mcm de 324, 16, 7 y 5 es 45360.

Galería de imágenes

  • Divisores 50 72

    Descomposición en factores primos de 72 y 50.

  • Divisores 6 33

    Descomposición en factores primos de 6 y 33.

Véase también

Kids robot.svg En inglés: Least common multiple Facts for Kids

Obtenido de «https://ninos.kiddle.co/index.php?title=Mínimo_común_múltiplo&oldid=4957139»
kids search engine
Todo el contenido de los artículos de la Enciclopedia Kiddle (incluidas las imágenes) se puede utilizar libremente para fines personales y educativos bajo la licencia Atribución-CompartirIgual a menos que se indique lo contrario. Citar este artículo:
Mínimo común múltiplo para Niños. Enciclopedia Kiddle.