Montserrat Teixidor i Bigas para niños

Montserrat Teixidor i Bigas es una investigadora española, profesora titular en el Departamento de Matemáticas de la Universidad de Tufts en Medford, Massachusetts. Teixidor obtuvo su doctorado en la Universidad de Barcelona (España) en 1986, y su tesis llevó por título "Geometría de sistemas lineales en curvas algebraicas", cuyo director fue Gerard Eryk Welters.

Trayectoria

Trabajó en el Departamento de Matemáticas puras en la Universidad de Liverpool (Reino Unido), donde en 1988 escribió el artículo "El divisor de curvas con un theta-null evanescente", que se publicó en la revista Compositio Mathematica. Teixidor, aceptó un puesto de profesora asociada de matemáticas en la Universidad de Tufts, y ha estado en la Facultad de Tufts desde 1989.

Su área de especialización es la geometría algebraica y especialmente los módulos de paquetes de vectores de curvas. También fue coorganizadora del grupo de trabajo del Instituto Clay de Matemáticas sobre paquetes de vectores de curvas. Entre 2004 y 2005, pasó un tiempo en el Instituto de Estudios Avanzados Radcliffe de la Universidad de Harvard como fellow de Vera M. Schuyler, dedicándose al estudio de "la interacción entre la geometría de las curvas y las ecuaciones que las definen".

Además, trabajó con Barbara Russo para probar la conjetura de Lange, que afirma que si , entonces existen paquetes de vectores estables con . Teixidor y Russo prueban este resultado para la curva genérica. También aclaran lo que sucede en el intervalo utilizando un argumento de degeneración a una curva reducible.

Publicaciones principales

• Montserrat Teixidor i Bigas, "Brill-Noether theory for vector bundles," Duke Math. J. Volume 62, Number 2 (1991), 385-400.
• Montserrat Teixidor i Bigas Curves en Grassmannians, Proc. Amer. Math. Soc. 126 (1998), no. 6, 1597–1603.
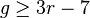
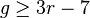• Montserrat Teixidor i Bigas "Green's conjecture for the generic -gonal curve of genus ," Duke Math. J.111 (2002), no. 2, 195–222.
• Montserrat Teixidor i Bigas Existencia de sistemas coherentes, Internat. J. Math. 19 (2008), no. 4, 449–454.
• Ivona Grzegorczyk, Montserrat Teixidor i Bigas, Brill-Noether theory for stable vector bundles, Moduli spaces and vector bundles, 29–50, London Math. Soc. Lecture Note Ser., 359, CUP, Cambridge (2009).
• Montserrat Teixidor i Bigas, Vector bundles on reducible curves and applications, Clay Mathematics Proceedings (2011).
• Tawanda Gwena, Montserrat Teixidor i Bigas, Maps between moduli spaces of vector bundles and the base locus of the theta divisor.
• Brian Osserman, Montserrat Teixidor i Bigas Linked alternating forms and linked symplectic Grassmannians, Int. Math. Res. No. IMRN 2014, no. 3, 720-744.

Véase también

En inglés: Montserrat Teixidor i Bigas Facts for Kids