Media aritmética para niños
La media aritmética es un concepto matemático muy útil en estadística. También se le llama promedio o simplemente media. Se calcula sumando un grupo de números y luego dividiendo el resultado entre la cantidad total de números que sumaste.
Además de en matemáticas y estadística, la media aritmética se usa mucho en economía, antropología, historia y en casi todas las áreas de estudio. Por ejemplo, la renta per cápita es el ingreso promedio de las personas en un país.
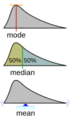
Aunque la media aritmética se usa para mostrar el "centro" de un grupo de datos, no siempre es la mejor opción si hay números muy diferentes. Si hay valores muy grandes o muy pequeños (llamados valores atípicos), la media aritmética puede verse muy afectada. Por ejemplo, en la distribución de ingresos, donde algunas personas ganan mucho más que la mayoría, la media aritmética podría no representar el ingreso "típico". En esos casos, otras medidas, como la mediana, pueden dar una idea más clara del centro de los datos.
Plantilla:Ficha de concepto
Contenido
¿Qué es la Media Aritmética?
La media aritmética es una de las medidas más comunes para encontrar el "centro" de un conjunto de datos. Imagina que tienes varias calificaciones de un examen y quieres saber tu promedio. La media aritmética te ayuda a encontrar ese número.
¿Cómo se Calcula la Media Aritmética?
Para calcular la media aritmética de un grupo de n números (por ejemplo,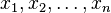 
), se usa la siguiente fórmula:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \bar{x} =\frac{x_1+x_2+\cdots+x_n}{n}
Aquí,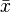 
(se lee "x barra") representa la media. Simplemente sumas todos los números y divides el resultado entre cuántos números hay.
Por ejemplo, si quieres calcular la media aritmética de 8, 5 y -1, harías lo siguiente:
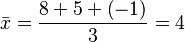
Así, la media aritmética de 8, 5 y -1 es 4.
Cuando hablamos de la media de una muestra (un grupo pequeño de datos), usamos el símbolo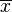 
. Si hablamos de la media de una población completa (todos los datos posibles), usamos la letra griega 
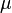(mu).
Ejemplos Prácticos
- Para encontrar la media aritmética de tres números, los sumas y divides el total entre 3.
- Para encontrar la media aritmética de cuatro números, los sumas y divides el total entre 4.
¿Para Qué Sirve la Media Aritmética?
La media aritmética es muy útil para resumir grandes cantidades de datos en un solo número. Nos da una idea rápida del valor "típico" o "promedio" de un conjunto. Por ejemplo, puedes usarla para:
- Calcular el promedio de tus calificaciones.
- Saber la altura promedio de los estudiantes en tu clase.
- Entender el promedio de goles anotados por un equipo de fútbol en una temporada.
¿Cuáles son las Propiedades de la Media Aritmética?
La media aritmética tiene algunas características importantes:
- Si sumas las diferencias de cada número con respecto a la media, el resultado siempre será cero. Esto significa que la media es como el punto de equilibrio de los datos.
- Si a todos los números de un grupo les sumas la misma cantidad, la media aritmética también aumentará en esa misma cantidad.
- Si todos los números de un grupo los multiplicas por la misma cantidad, la media aritmética también se multiplicará por esa cantidad.
- La media aritmética siempre estará entre el número más pequeño y el número más grande del grupo de datos.
- La media no tiene por qué ser uno de los números originales, y puede ser un número decimal aunque los datos originales sean enteros.
- La media es un valor que representa al grupo de datos. Nos ayuda a comparar diferentes grupos.
Por ejemplo, si en una reunión hay 38 personas, y queremos saber cuántas nacieron en el mismo mes, podemos calcular el promedio: 38 personas / 12 meses ≈ 3.167 personas por mes. Esto nos dice que al menos 4 personas nacieron en el mismo mes, porque no puede haber una fracción de persona.
Media Aritmética vs. Mediana: ¿Cuál es la Diferencia?
La media aritmética a veces se confunde con la mediana. La mediana es el número que está justo en el medio de un grupo de datos cuando los ordenas de menor a mayor. La mitad de los números son más grandes que la mediana y la otra mitad son más pequeños.
Si los números de un grupo aumentan de forma constante (como 1, 2, 3, 4), la media y la mediana serán iguales. Por ejemplo, para {1, 2, 3, 4}, la media es 2.5 y la mediana también es 2.5.
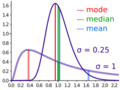
Pero si los números no aumentan de forma constante (como {1, 2, 4, 8, 16}), la media y la mediana pueden ser muy diferentes. En este caso, la media es 6.2, mientras que la mediana es 4. Esto muestra que la media puede ser muy diferente de la mayoría de los valores si hay números extremos.
Tipos Especiales de Promedios
Promedio Ponderado
A veces, no todos los números tienen la misma importancia. Un promedio ponderado es cuando a algunos números se les da más "peso" que a otros. Por ejemplo, si en tu calificación final un examen vale el doble que una tarea, el examen tiene más peso.
La media aritmética "normal" es un caso especial del promedio ponderado, donde todos los números tienen el mismo peso.
Promedio de Ángulos
Cuando trabajamos con datos que son cíclicos, como los ángulos (por ejemplo, grados en un círculo), hay que tener cuidado. Si calculas la media aritmética de 1° y 359°, obtendrías 180°. Pero esto no es lo más lógico, porque 0° (o 360°) está mucho más cerca de ambos ángulos (a solo 1° de distancia) que 180° (a 179° de distancia).
En estos casos, se usan métodos especiales para encontrar el promedio que tenga más sentido geométricamente, considerando que los ángulos se repiten cada 360°.
Símbolos Comunes
La media aritmética se representa a menudo con una letra (como la x) y una barra horizontal encima (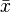). Esta barra se llama "vinculum" o "macrón".
A veces, en algunos programas de computadora o navegadores web, el símbolo 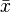puede no mostrarse correctamente. Esto ocurre porque el símbolo se forma combinando la letra "x" con un código para la línea superior.
Galería de imágenes
-
Prueba sin palabras de la desigualdad de las medias aritmética y geométrica.
-
Prueba geométrica sin palabras de la relación entre las medias cuadrática, aritmética, geométrica y armónica.
Véase también
En inglés: Mean Facts for Kids
