Magma (álgebra) para niños

Un magma es un concepto de las matemáticas que nos ayuda a entender cómo funcionan algunas operaciones. Imagina que tienes un grupo de cosas, como números o letras, y una regla para combinarlas. Un magma es justo eso: un conjunto (un grupo de elementos) y una sola operación matemática que puedes usar con esos elementos.

La regla más importante para esta operación es que, cuando combinas dos elementos del conjunto, el resultado siempre debe ser otro elemento que también pertenezca a ese mismo conjunto. Por ejemplo, si tienes solo números enteros y la operación es la suma, al sumar dos números enteros, el resultado siempre será otro número entero. Esto se llama una operación interna.

El nombre "magma" fue propuesto por un grupo de matemáticos franceses llamado Nicolás Bourbaki. Antes, a veces se usaba la palabra "grupoide", pero esa palabra ahora se usa para otra cosa en matemáticas, así que es mejor usar "magma" para este concepto.

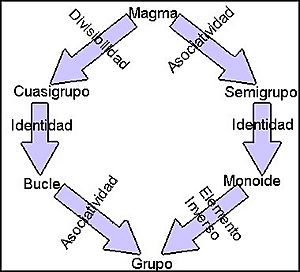
¿Qué tipos de magmas existen?

De magma a grupo.

Existen diferentes tipos de magmas, cada uno con reglas adicionales que hacen su operación más específica. Piensa en ellos como "familias" de magmas:

• Cuasigrupos: Son magmas donde siempre puedes "deshacer" la operación. Es decir, si conoces el resultado y uno de los elementos, puedes encontrar el otro.
• Bucles: Son cuasigrupos que tienen un "elemento neutro". Un elemento neutro es como el cero en la suma (0 + 5 = 5) o el uno en la multiplicación (1 * 5 = 5); no cambia el otro elemento cuando se opera con él.
• Semigrupos: Son magmas donde la operación es "asociativa". Esto significa que no importa cómo agrupes los elementos al operar más de dos, el resultado será el mismo. Por ejemplo, (2 + 3) + 4 es igual a 2 + (3 + 4).
• Monoides: Son semigrupos que también tienen un elemento neutro.
• Grupos: Son monoides que, además, tienen "elementos simétricos". Un elemento simétrico es como el opuesto en la suma (5 + (-5) = 0) o el inverso en la multiplicación (5 * (1/5) = 1); al operarlo con otro elemento, te da el elemento neutro.
• Grupos abelianos: Son grupos donde la operación es "conmutativa". Esto significa que el orden de los elementos no importa. Por ejemplo, 2 + 3 es igual a 3 + 2.

Magmas y la no asociatividad

Una operación en un magma puede ser "no asociativa". Esto significa que el orden en que realizas las operaciones sí importa. Si tienes tres elementos y una operación no asociativa, (A * B) * C no es lo mismo que A * (B * C).

Por ejemplo, la resta y la división de números son operaciones no asociativas:

• (10 - 5) - 2 = 5 - 2 = 3
• 10 - (5 - 2) = 10 - 3 = 7

Como ves, los resultados son diferentes.

Cuando una operación es no asociativa, usamos paréntesis para indicar qué operación se debe hacer primero. Sin embargo, a veces los matemáticos y programadores acuerdan un orden específico para algunas operaciones comunes.

Ejemplos de operaciones no asociativas

Algunas operaciones se evalúan de izquierda a derecha:

• Resta y división de números reales:
  • 10 - 5 - 2 se entiende como (10 - 5) - 2.
  • 10 / 5 / 2 se entiende como (10 / 5) / 2.

Otras operaciones se evalúan de derecha a izquierda:

• Exponenciación de números reales:
  • 2³² se entiende como 2⁽³²⁾, que es 2⁹ = 512.
  • Si fuera de izquierda a derecha, sería (2³)² = 8² = 64, lo cual es diferente.
• El operador de asignación en programación: En lenguajes como C, si escribes `x = y = z;`, significa que primero `z` se asigna a `y`, y luego el valor de `y` (que ahora es `z`) se asigna a `x`.

Hay otras operaciones no asociativas para las que no hay un orden establecido, por lo que siempre se necesitan paréntesis:

• Calcular el promedio de números: El promedio de (x, y) y luego z no es lo mismo que x y luego el promedio de (y, z).
• Tomar el complemento relativo de conjuntos: (A \ B) \ C no es lo mismo que A \ (B \ C).

Véase también

En inglés: Magma (algebra) Facts for Kids

• Categoría de los magmas