Intervalo (música) para niños
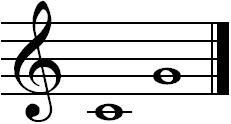
Un intervalo en la música es la distancia que hay entre dos notas musicales diferentes. Esta distancia se mide por la diferencia en la altura de los sonidos, es decir, qué tan agudo o grave es un sonido comparado con otro. Para entenderlo mejor, piensa en las notas de una escala, como Do, Re, Mi, Fa, Sol, La, Si. Si cuentas desde una nota hasta otra, incluyendo ambas, puedes saber qué tipo de intervalo es. Por ejemplo, entre la nota re y la nota fa, hay una distancia de tres notas (re, mi, fa), por eso se le llama una tercera.
Contenido
¿Cómo se estudiaron los intervalos en el pasado?
Desde hace mucho tiempo, las personas han estado interesadas en cómo funcionan los intervalos musicales.
Primeros estudios y herramientas
Los primeros estudios conocidos sobre los intervalos fueron hechos por pensadores como Aristóxeno de Tarento en la antigua Grecia. Él usaba tanto la observación como las matemáticas para entender la música. Otros, como Pitágoras, también exploraron las relaciones matemáticas de los sonidos.
Antiguamente, se usaba un instrumento llamado monocordio para enseñar y entender los intervalos. Este instrumento tenía una sola cuerda y permitía a los músicos y científicos ver cómo cambiaban los sonidos al variar la longitud de la cuerda.
Avances en el cálculo musical
En el siglo XVI, un investigador llamado Simon Stevin estudió cómo calcular las frecuencias de los sonidos y los intervalos usando fórmulas matemáticas. Más tarde, en el siglo XVII, Francesco Cavalieri y Juan Caramuel aplicaron un tipo de cálculo llamado logaritmos para entender mejor estas relaciones.
En el siglo XIX, Hermann Helmholtz construyó unos aparatos llamados resonadores. Estos aparatos ayudaron a demostrar que todos los sonidos musicales son complejos y están formados por varios sonidos más pequeños, llamados armónicos. Estos armónicos tienen intervalos que coinciden con los que se pueden demostrar con un monocordio.
Tipos de intervalos musicales
Los intervalos se pueden clasificar de varias maneras, lo que nos ayuda a entenderlos mejor.
Intervalos simples y compuestos
Un intervalo puede ser:
- Simple: Si la distancia entre las dos notas no es mayor que una octava. Una octava es cuando una nota se repite pero más aguda o más grave (por ejemplo, de Do a otro Do más agudo).
- Compuesto: Si la distancia entre las dos notas es mayor que una octava.
Los intervalos compuestos son como los simples, pero con una o más octavas añadidas. Por ejemplo, una novena es como una segunda, pero una octava más arriba. Una duodécima es como una quinta, pero una octava más arriba.
Nombres de los intervalos simples
Los intervalos simples tienen nombres específicos según la cantidad de notas que los forman:
| Nombre del intervalo | Distancia en tonos y semitonos |
|---|---|
| Unísono | Mismo sonido (0 tonos) |
| Segunda menor | 1 semitono |
| Segunda mayor | 1 tono |
| Tercera menor | 1 tono y medio |
| Tercera mayor | 2 tonos |
| Cuarta justa | 2 tonos y medio |
| Cuarta aumentada (también llamada tritono) | 3 tonos |
| Quinta justa | 3 tonos y medio |
| Sexta menor | 4 tonos |
| Sexta mayor | 4 tonos y medio |
| Séptima menor | 5 tonos |
| Séptima mayor | 5 tonos y medio |
| Octava justa | 6 tonos |
Los intervalos también pueden ser mayores o menores.
- Los intervalos mayores suelen sonar más alegres.
- Los intervalos menores suelen sonar más serios o tristes.
Intervalos melódicos y armónicos

U = unísono (dos notas iguales)
m2 = de segunda menor (1st)
M2 = de segunda mayor (1T)
m3 = de tercera menor (1T 1st)
M3 = de tercera mayor (2T)
P4 = de cuarta justa o perfecta (2T 1st)
TT = de cuarta aumentada o tritono (2T 2st)
P5 = de quinta justa o perfecta (3T 1st)
m6 = de sexta menor (3T 2st)
M6 = de sexta mayor (4T 1st)
m7 = de séptima menor (4T 2st)
M7 = de séptima mayor (5T 1st)
P8 = de octava justa o perfecta (5T 2st)
Con la segunda nota en la siguiente octava y manteniendo la fundamental se generan los intervalos de novena, que equivale con una octava de diferencia al de segunda, el de undécima, que equivale al de cuarta, el de treceava, que equivale al de sexta, etc.
Un intervalo puede ser:
- Armónico: Si las dos notas suenan al mismo tiempo. Piensa en un acorde de guitarra o piano.
- Melódico: Si las dos notas suenan una después de la otra. Esto es lo que escuchas en una melodía. Los intervalos melódicos pueden ser ascendentes (la segunda nota es más aguda) o descendentes (la segunda nota es más grave).
Intervalos conjuntos y disjuntos
Esta clasificación se usa para los intervalos melódicos:
- Conjunto: Si las dos notas están una al lado de la otra en una escala, como Do y Re. También se les llama "pasos".
- Disjunto: Si las dos notas no están una al lado de la otra en una escala, como Do y Mi. También se les llama "saltos".
En la escala diatónica, un paso es una segunda (menor o mayor). Cualquier intervalo más grande que una segunda es un salto. Por ejemplo, de Do a Re es un paso, mientras que de Do a Mi es un salto.
Intervalos diatónicos y cromáticos
Un intervalo puede ser:
- Diatónico: Cuando está formado por dos notas que pertenecen a una escala diatónica (como la escala de Do mayor).
- Cromático: Cuando está formado por dos notas que pertenecen a una escala cromática. Una escala cromática incluye todas las notas, tanto las naturales como las sostenidas o bemoles.
Por ejemplo, la quinta justa entre La bemol y Mi bemol es cromática para la escala de Do mayor, porque esas notas no están en la escala de Do mayor. Sin embargo, es diatónica si la consideramos dentro de la escala de La bemol mayor.
Intervalos consonantes y disonantes
Consonancia y disonancia son términos que describen si un intervalo suena estable y en "reposo" (consonante) o si suena tenso y necesita "resolverse" (disonante). La idea de qué es consonante o disonante ha cambiado mucho a lo largo de la historia de la música.
- En la Edad Media, la cuarta justa se consideraba muy consonante. Sin embargo, la cuarta aumentada, llamada "tritono", se consideraba muy disonante y hasta se le llamaba "el diablo en la música".
- En la armonía tradicional, que se desarrolló a partir del siglo XVII, algunos intervalos se consideran más estables que otros.
* Consonancias perfectas: Cuartas, quintas y octavas justas. * Consonancias imperfectas: Terceras y sextas (mayores o menores). * Disonancias: Segundas, séptimas y la mayoría de los intervalos aumentados o disminuidos.
Estos conceptos son importantes para los compositores, ya que usan la tensión y la relajación de los intervalos para crear diferentes sensaciones en la música.
Frecuencias de los intervalos
La diferencia de frecuencia entre las dos notas de un intervalo se puede medir con una relación matemática. Por ejemplo, una octava tiene una relación de frecuencia de 2:1, lo que significa que la nota más aguda vibra el doble de rápido que la más grave. Otros intervalos justos también tienen relaciones simples, como la quinta justa (3:2) o la cuarta justa (4:3).
Inversión de intervalos
Un intervalo se puede invertir subiendo la nota de abajo una octava o bajando la nota de arriba una octava. Por ejemplo, si tienes un Do grave y un Fa más agudo (una cuarta), puedes invertirlo subiendo el Do una octava. Entonces tendrías un Fa grave y un Do más agudo, que es una quinta.
Hay algunas reglas para entender las inversiones:
- La suma del número de un intervalo y el número de su inversión siempre es nueve. Por ejemplo, una cuarta (4) y una quinta (5) suman 9.
- La inversión de un intervalo mayor es uno menor (y viceversa).
- La inversión de un intervalo justo es otro justo.
- La inversión de un intervalo aumentado es uno disminuido (y viceversa).
Galería de imágenes
-
Escala de la bemol mayor
Véase también
 En inglés: Interval (music) Facts for Kids
En inglés: Interval (music) Facts for Kids
- Acústica musical
- Afinación pitagórica
- Acordes
- Escalas