Intervalo (matemática) para niños
Un intervalo (del latín intervallum) es un grupo especial de números en la recta numérica. Imagina un segmento continuo de números sin espacios. Si eliges dos números cualesquiera dentro de este grupo, todos los números que están entre ellos también forman parte del grupo.
Contenido
¿Qué es un Intervalo?
Un intervalo es un conjunto de números reales que cumple una regla sencilla: si tomas dos números que pertenecen al intervalo, cualquier otro número que se encuentre entre ellos también debe pertenecer al mismo intervalo. Esto significa que los intervalos no tienen "agujeros" o interrupciones.
Tipos de Intervalos y su Notación
Para escribir los intervalos, usamos corchetes `[` o `]` y paréntesis `(` o `)`. La forma en que los usamos nos dice si los números de los extremos están incluidos o no.
Intervalos Abiertos
Un intervalo abierto no incluye los números de sus extremos. Se representa con paréntesis `(` y `)`. Por ejemplo, el intervalo `(a,b)` incluye todos los números entre `a` y `b`, pero no incluye ni `a` ni `b`.
- Notación: `(a,b)` o `]a,b[`
- Significado: Todos los números `x` tales que `a < x < b`.
- Ejemplo: `(2,5)` incluye números como 2.1, 3, 4.9, pero no 2 ni 5.
Intervalos Cerrados
Un intervalo cerrado sí incluye los números de sus extremos. Se representa con corchetes `[` y `]`. Por ejemplo, el intervalo `[a,b]` incluye todos los números entre `a` y `b`, y también incluye `a` y `b`.
- Notación: `[a,b]`
- Significado: Todos los números `x` tales que `a ≤ x ≤ b`.
- Ejemplo: `[2,5]` incluye números como 2, 2.1, 3, 4.9, y 5.
Intervalos Semiabiertos
Los intervalos semiabiertos incluyen solo uno de sus extremos. Pueden ser:
- Cerrado a la izquierda y abierto a la derecha: Incluye el primer número, pero no el segundo.
- Notación: `[a,b)` o `[a,b[`
- Significado: Todos los números `x` tales que `a ≤ x < b`.
- Ejemplo: `[2,5)` incluye 2, pero no 5.
- Abierto a la izquierda y cerrado a la derecha: No incluye el primer número, pero sí el segundo.
- Notación: `(a,b]` o `]a,b]`
- Significado: Todos los números `x` tales que `a < x ≤ b`.
- Ejemplo: `(2,5]` incluye 5, pero no 2.
Estos cuatro tipos de intervalos se llaman finitos porque tienen un principio y un final definidos. Su "largo" se calcula restando el número final menos el inicial (`b - a`).
Intervalos con Infinito
A veces, un intervalo no tiene un límite en uno de sus lados. Esto se indica con el símbolo de infinito (`∞`). Como el infinito no es un número real, nunca se incluye en el intervalo, por lo que siempre se usa un paréntesis junto a él.
- Desde un número hasta el infinito positivo:
- Incluyendo el extremo: `[a,∞)` o `[a,∞[`
- Significado: Todos los números `x` tales que `x ≥ a`.
- Ejemplo: `[3,∞)` incluye 3 y todos los números mayores que 3.
- Incluyendo el extremo: `[a,∞)` o `[a,∞[`
-
- Sin incluir el extremo: `(a,∞)` o `]a,∞[`
- Significado: Todos los números `x` tales que `x > a`.
- Ejemplo: `(3,∞)` incluye todos los números mayores que 3, pero no 3.
- Sin incluir el extremo: `(a,∞)` o `]a,∞[`
- Desde el infinito negativo hasta un número:
- Incluyendo el extremo: `(-∞,a]` o `]-∞,a]`
- Significado: Todos los números `x` tales que `x ≤ a`.
- Ejemplo: `(-∞,7]` incluye 7 y todos los números menores que 7.
- Incluyendo el extremo: `(-∞,a]` o `]-∞,a]`
-
- Sin incluir el extremo: `(-∞,a)` o `]-∞,a[`
- Significado: Todos los números `x` tales que `x < a`.
- Ejemplo: `(-∞,7)` incluye todos los números menores que 7, pero no 7.
- Sin incluir el extremo: `(-∞,a)` o `]-∞,a[`
- Todos los números reales:
- Notación: `(-∞,∞)` o `]-∞,∞[`
- Significado: Incluye todos los números reales. Es la recta numérica completa.
Operaciones con Intervalos
Podemos combinar intervalos usando operaciones como la unión y la intersección, igual que con otros conjuntos.
Unión de Intervalos
La unión de dos o más intervalos (`A ∪ B`) es un nuevo conjunto que incluye todos los números que están en cualquiera de los intervalos originales.
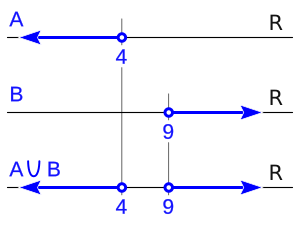
- Ejemplo: Si `A = (-∞,4)` (todos los números menores que 4) y `B = (9,∞)` (todos los números mayores que 9).
- La unión `A ∪ B` sería `(-∞,4) ∪ (9,∞)`. Esto significa que un número está en este conjunto si es menor que 4 O es mayor que 9.
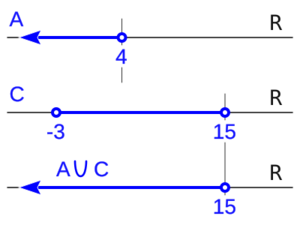
- Otro ejemplo: Si `A = (-∞,4)` y `C = (-3,15)`.
- La unión `A ∪ C` sería `(-∞,15)`. Esto es porque `C` "cubre" la parte de `A` que va de -3 a 4, y se extiende hasta 15.
Intersección de Intervalos
La intersección de dos o más intervalos (`A ∩ B`) es un nuevo conjunto que incluye solo los números que están en TODOS los intervalos originales al mismo tiempo.
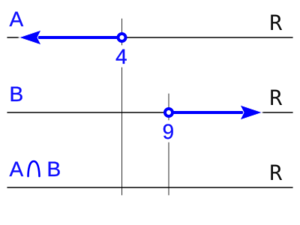
- Ejemplo: Si `A = (-∞,4)` y `B = (9,∞)`.
- La intersección `A ∩ B` es el conjunto vacío (`∅`). Esto significa que no hay ningún número que sea menor que 4 Y, al mismo tiempo, mayor que 9. No tienen números en común.
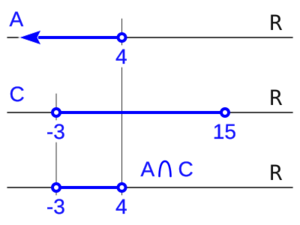
- Otro ejemplo: Si `A = (-∞,4)` y `C = (-3,15)`.
- La intersección `A ∩ C` sería `(-3,4)`. Estos son los números que están en ambos intervalos: son mayores que -3 Y menores que 4.
Entornos: Espacios Alrededor de un Punto
Un entorno de un punto es un intervalo abierto que rodea a ese punto. Nos ayuda a entender qué números están "cerca" de un punto específico.
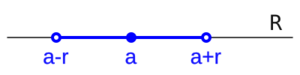
Entorno Simétrico
Un entorno simétrico de un punto `a` con un radio `r` es un intervalo que se extiende la misma distancia a ambos lados de `a`.
- Notación: `E(a,r)`
- Significado: `(a-r, a+r)`. Incluye todos los números `x` cuya distancia a `a` es menor que `r`.
- Ejemplo: `E(0,1)` es el intervalo `(-1,1)`. Incluye todos los números entre -1 y 1.
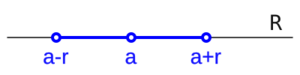
Entorno Reducido
Un entorno reducido es un entorno simétrico al que se le quita el punto central.
- Notación: `E*(a,r)`
- Significado: `(a-r, a+r)` sin el punto `a`.
- Ejemplo: `E*(0,1)` es `(-1,0) ∪ (0,1)`. Incluye todos los números entre -1 y 1, excepto el 0.
Casos Especiales de Intervalos
- Si en un intervalo `(a,b)` el número `a` es mayor que `b` (por ejemplo, `(5,2)`), el intervalo no tiene elementos y representa el conjunto vacío.
- Los intervalos `(a,a)`, `[a,a)`, y `(a,a]` también representan el conjunto vacío.
- El intervalo `[a,a]` representa un conjunto unitario, es decir, un conjunto que contiene un solo número: `{a}`. A esto se le llama un intervalo degenerado.
Propiedades Importantes de los Intervalos
- La unión de varios intervalos no siempre forma un solo intervalo. Por ejemplo, `(-∞,4) ∪ (9,∞)` son dos partes separadas.
- Los intervalos son "conexos" en la recta numérica, lo que significa que no tienen interrupciones.
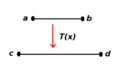
- Si aplicas una función continua a un intervalo, el resultado también será un intervalo. Esto es parte del Teorema del valor intermedio.
Aritmética con Intervalos
Podemos hacer operaciones básicas con intervalos. Si tenemos `I=[a,b]` y `J=[c,d]`:
- Suma: `I + J = [a+c, b+d]`
- Resta: `I - J = [a-d, b-c]`
- Multiplicación: Si todos los números `a, b, c, d` son positivos, `I · J = [ac, bd]`
- División: Si todos los números `a, b, c, d` son positivos, `I / J = [a/d, b/c]`
Más Allá de la Recta Numérica
Los intervalos no solo existen en una línea. Podemos tener intervalos en más dimensiones. Por ejemplo, un intervalo en 2 dimensiones sería un rectángulo en un plano cartesiano, formado por la combinación de dos intervalos, uno para el eje X y otro para el eje Y.
Galería de imágenes
Véase también
 En inglés: Interval (mathematics) Facts for Kids
En inglés: Interval (mathematics) Facts for Kids









 y radio
y radio  .
.