Función monótona para niños
Una función monótona es un tipo especial de función matemática que sigue un patrón constante en su comportamiento. Imagina que estás subiendo o bajando una colina: una función monótona siempre va en una dirección, o siempre sube, o siempre baja, o se mantiene en el mismo nivel. Nunca cambia de dirección.
Este concepto se usa mucho en diferentes áreas de las matemáticas, como el cálculo (que estudia cómo cambian las cosas) y la teoría del orden (que se ocupa de cómo se organizan los elementos en un conjunto). Aunque los nombres pueden variar un poco entre estas áreas, la idea principal es la misma: la función mantiene el orden de los números.
Contenido
¿Qué es una Función Monótona?
Una función, que podemos llamar f, toma un número de un conjunto (por ejemplo, el conjunto de los números reales) y lo transforma en otro número. Decimos que una función f es monótona si cumple una de estas dos condiciones:
- Es creciente: Si tomas dos números, digamos x e y, y x es menor o igual que y (x ≤ y), entonces el resultado de la función para x (f(x)) también será menor o igual que el resultado para y (f(y)). Es decir, si los números de entrada aumentan, los resultados de la función también aumentan (o se mantienen iguales).
- Es decreciente: Si x es menor o igual que y (x ≤ y), entonces el resultado de la función para x (f(x)) será mayor o igual que el resultado para y (f(y)). En este caso, si los números de entrada aumentan, los resultados de la función disminuyen (o se mantienen iguales).
En resumen, una función es monótona si siempre "conserva el orden" de los números, ya sea manteniéndolos en el mismo sentido (creciente) o invirtiéndolos (decreciente).
¿Qué significa "Estrictamente Monótona"?
A veces, una función es aún más estricta en su comportamiento:
- Estrictamente creciente: Si x es estrictamente menor que y (x < y), entonces f(x) es estrictamente menor que f(y) (f(x) < f(y)). Esto significa que la función siempre sube, nunca se mantiene en el mismo nivel.
- Estrictamente decreciente: Si x es estrictamente menor que y (x < y), entonces f(x) es estrictamente mayor que f(y) (f(x) > f(y)). Esto significa que la función siempre baja, nunca se mantiene en el mismo nivel.
Cuando una función es estrictamente creciente o estrictamente decreciente, se le llama estrictamente monótona.
Funciones Monótonas en Lógica
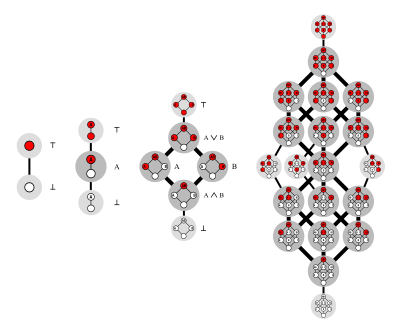
Las funciones monótonas también aparecen en el álgebra de Boole, que es una parte de la lógica matemática que trabaja con valores de "verdadero" (1) y "falso" (0).
Una función booleana es monótona si, al cambiar una entrada de 0 a 1, la salida de la función nunca cambia de 1 a 0. Es decir, si las entradas "aumentan" (de 0 a 1), la salida de la función solo puede aumentar (de 0 a 1) o quedarse igual.
Estas funciones son especiales porque se pueden construir usando solo operaciones lógicas como "y" (conjunción) y "o" (disyunción), sin usar la operación de "no" (negación).
El número de estas funciones monótonas para un cierto número de variables se conoce como el número de Dedekind.
Galería de imágenes
Véase también
 En inglés: Monotonic function Facts for Kids
En inglés: Monotonic function Facts for Kids