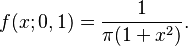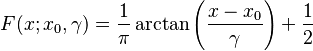Distribución de Cauchy para niños
La distribución de Cauchy-Lorentz es un concepto importante en las matemáticas y la física. Lleva el nombre de dos científicos famosos: Augustin Cauchy y Hendrik Lorentz.
También se le conoce como distribución de Cauchy en el campo de la estadística. En física, se le llama distribución de Lorentz o función Lorentziana. Es muy útil porque ayuda a describir cómo se comportan ciertos fenómenos, como la resonancia forzada. En la espectroscopia, que es el estudio de cómo la luz interactúa con la materia, esta distribución explica la forma de las líneas de luz que vemos, especialmente cuando se ensanchan por colisiones.
Datos para niños Cauchy-Lorentz |
||
|---|---|---|
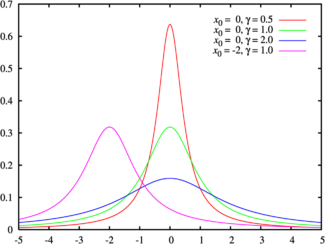 La línea verde es la distribución estándar de Cauchy Función de densidad de probabilidad |
||
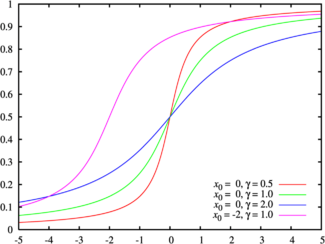 Leyenda de colores para la PDF de la imagen superior Función de distribución de probabilidad |
||
| Parámetros | 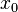 (real) (real)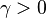 escala (real) escala (real) |
|
| Función de densidad (pdf) | ![\frac{1}{\pi\gamma\,\left[1 + \left(\frac{x-x_0}{\gamma}\right)^2\right]} \!](/images/math/1/1/0/110abf1f3bbdd637b6ddd41296caa067.png) |
|
| Función de distribución (cdf) | 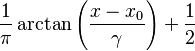 |
|
| Media | no definida | |
| Mediana | 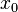 |
|
| Moda | 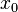 |
|
| Varianza | no definida | |
| Curtosis | no definida | |
| Entropía | 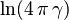 |
|
| Función generadora de momentos (mgf) | no definida | |
| Función característica | 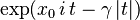 |
|
Contenido
¿Cómo se describe la distribución de Cauchy?
La función de densidad de probabilidad
En estadística, la distribución de Cauchy es una forma de describir cómo se distribuyen los datos de manera continua. Su función de densidad de probabilidad (FDP) es una fórmula matemática que nos dice qué tan probable es que un valor específico aparezca en la distribución.
La fórmula general es:
Aquí, x0 es el punto central o "pico" de la distribución. El símbolo γ (gamma) nos dice qué tan ancha es la distribución.
Cuando x0 es 0 y γ es 1, se le llama la distribución estándar de Cauchy. Su fórmula es más sencilla:
Una característica especial de la distribución de Cauchy es que no tiene un valor promedio (media) ni una varianza (que mide qué tan dispersos están los datos) definidos.
La función de distribución acumulativa
La función de distribución acumulativa (FDA) nos dice la probabilidad de que un valor sea menor o igual a un número dado. Para la distribución de Cauchy, la FDA es:
¿Qué características tiene la distribución de Cauchy?
La distribución de Cauchy es única porque, a diferencia de muchas otras distribuciones, no tiene un valor esperado (media) ni una varianza definidos. Esto significa que no podemos calcular un promedio típico para ella.
Sin embargo, su moda (el valor que aparece con más frecuencia) y su mediana (el valor central cuando los datos están ordenados) sí están bien definidas. Ambas son iguales a x0, el punto central de la distribución.
Un dato interesante es que si tomas dos variables aleatorias independientes que siguen una Distribución normal (como la curva de campana) con un promedio de 0 y una varianza de 1, y divides una por la otra, el resultado tendrá una distribución estándar de Cauchy.
Además, si tienes varias variables aleatorias que siguen una distribución de Cauchy y calculas su promedio, ¡ese promedio también seguirá una distribución de Cauchy! Esto es diferente a lo que ocurre con otras distribuciones y muestra lo especial que es la distribución de Cauchy.
La distribución de Cauchy es un tipo de distribución que se llama "infinitamente divisible" y "estable".
¿Para qué se usa la distribución de Cauchy?
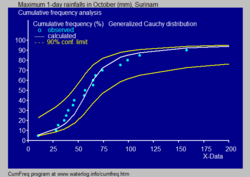
- En el estudio del agua (conocido como hidrología), la distribución de Cauchy se usa para analizar datos como las lluvias máximas diarias o el caudal de los ríos. También puede ayudar a describir períodos de sequía.
La imagen azul que ves muestra cómo se puede usar la distribución de Cauchy para entender los datos de lluvias máximas diarias. La línea azul representa la distribución, y la zona sombreada muestra un rango de confianza del 90%. Los puntos son los datos reales observados.
Véase también
 En inglés: Cauchy distribution Facts for Kids
En inglés: Cauchy distribution Facts for Kids
- Parametrización de McCullagh de las distribuciones de Cauchy


![\begin{align}
f(x; x_0,\gamma) &= \frac{1}{\pi\gamma \left[1 + \left(\frac{x-x_0}{\gamma}\right)^2\right]} \\[0.5em]
&= { 1 \over \pi } \left[ { \gamma \over (x - x_0)^2 + \gamma^2 } \right]
\end{align}](/images/math/c/9/6/c963d5240e57e4b0a2f14e7c93b9a223.png)