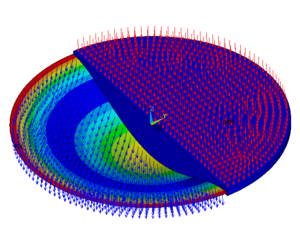
Ecuación en derivadas parciales para niños
Una ecuación en derivadas parciales (a veces llamada EDP) es un tipo especial de ecuación matemática. Imagina que tienes una función que depende de varias cosas al mismo tiempo, como la temperatura en un lugar (que cambia con la posición y el tiempo) o el sonido (que se mueve en el espacio y el tiempo).
Las EDPs son ecuaciones que no solo incluyen esa función, sino también cómo cambia esa función en diferentes direcciones o momentos. Es como si te preguntaran no solo cuál es la temperatura, sino también qué tan rápido está subiendo o bajando en un punto específico o en un momento dado.
Estas ecuaciones son muy importantes en la física y otras ciencias. Nos ayudan a entender y describir fenómenos que ocurren en el espacio y el tiempo, como:
- La forma en que el sonido se propaga.
- Cómo se distribuye el calor en un objeto.
- El movimiento de los fluidos (como el agua o el aire).
- Cómo se comportan los materiales elásticos (como una goma que se estira).
Matemáticos como los franceses d'Alembert y Fourier fueron pioneros en el estudio de estas ecuaciones.
A veces, encontrar la solución exacta para una EDP es muy difícil, ¡casi imposible de escribir con una fórmula simple! Por eso, los científicos y matemáticos usan computadoras para encontrar soluciones aproximadas. También hay mucha investigación para entender las características generales de estas soluciones, como si siempre existen, si son únicas o si son estables.
Las EDPs son fundamentales en muchos campos científicos, desde la ingeniería hasta la mecánica cuántica. Nos ayudan a comprender el mundo que nos rodea de una manera muy profunda.
Contenido
¿Qué es una Ecuación en Derivadas Parciales?
Una EDP es una ecuación que involucra una función desconocida que depende de dos o más variables y sus derivadas parciales. Una derivada parcial nos dice cómo cambia una función cuando solo una de sus variables cambia, manteniendo las otras constantes.
Por ejemplo, si tenemos una función u que depende de x e y (como u(x,y)), una EDP podría ser algo como: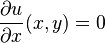 
Esto significa que la función u no cambia cuando movemos solo en la dirección de x. La solución a esta ecuación sería una función que solo depende de y, por ejemplo, u(x,y) = f(y), donde f puede ser cualquier función.
A diferencia de las ecuaciones más simples (llamadas ecuaciones diferenciales ordinarias), las soluciones de las EDPs a menudo no son únicas. Para encontrar una solución específica, necesitamos más información, como las "condiciones de contorno", que nos dicen cómo se comporta la función en los límites de un área o en un momento inicial.
Notación y ejemplos sencillos
Para escribir las derivadas parciales de forma más corta, a menudo se usan subíndices. Por ejemplo:
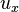significa la derivada de u con respecto a x.- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): u_{xy} significa la derivada de u primero con respecto a x y luego con respecto a y.
En física, a veces se usa el símbolo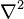 
(llamado laplaciano) para las derivadas espaciales y un punto sobre la letra (
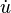) para las derivadas con respecto al tiempo. Por ejemplo, la ecuación de onda (que describe cómo se propagan las ondas, como el sonido) se puede escribir de forma compacta.
Tipos de EDPs de segundo orden
Las EDPs de segundo orden (aquellas que involucran derivadas hasta el segundo orden) se clasifican en varios tipos importantes, cada uno con propiedades y aplicaciones distintas. Los tres tipos principales son:
EDPs Elípticas
Estas ecuaciones suelen describir situaciones de equilibrio o estados estables. Un ejemplo famoso es la ecuación de Laplace, que se usa para entender la distribución de la temperatura en un objeto cuando ya no hay cambios, o el comportamiento de campos eléctricos sin movimiento.
- Ecuación de Laplace:
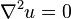
- Ecuación de Poisson:
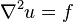(similar a la de Laplace, pero con una fuente o causa)
EDPs Hiperbólicas
Estas ecuaciones describen fenómenos que se propagan o se mueven, como las ondas. El ejemplo más conocido es la ecuación de onda.
- Ecuación de Onda:
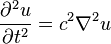(donde c es la velocidad de la onda)
EDPs Parabólicas
Estas ecuaciones se usan para describir procesos de difusión, donde algo se extiende o se dispersa con el tiempo, como el calor que se propaga en un material o la difusión de una sustancia.
- Ecuación de Difusión (o del Calor):
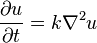(donde k es una constante de difusión)
La clasificación de una EDP de segundo orden se basa en los coeficientes de sus derivadas, de forma similar a cómo se clasifican las cónicas en geometría analítica (elipse, parábola, hipérbola).
EDPs de orden superior
Aunque las EDPs de segundo orden son muy comunes, existen otras que involucran derivadas de orden superior (tercera, cuarta, etc.). Estas se usan para describir fenómenos más complejos, como:
- La flexión de una placa elástica (cómo se dobla una lámina delgada).
- La vibración de una viga (cómo se mueve una barra larga y delgada).
Galería de imágenes
-
Flexión elástica de una placa circular empotrada en su contorno bajo la acción de una carga vertical distribuida uniformemente, que es solución de la ecuación de Lagrange de placas; la solución mostrada fue obtenida numéricamente mediante Ansys.
-
Variación del perfil de temperaturas solución de la ecuación del calor en un problema bidimensional
Véase también
En inglés: Partial differential equation Facts for Kids
