Distribución χ² para niños
Datos para niños Distribución χ² (ji al cuadrado) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
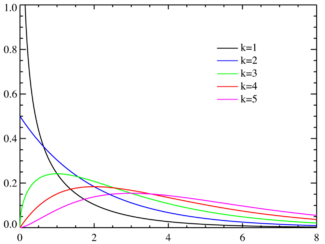 Función de densidad de probabilidad |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
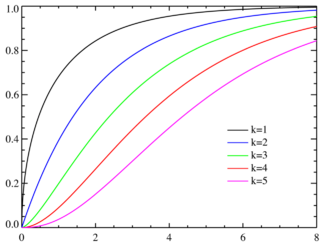 Función de distribución de probabilidad |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Parámetros | Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): k\in (0,\infty) grados de libertad | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Dominio | Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x\in(0,\infty) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Función de densidad (pdf) |
Esta distribución es muy importante en la estadística, especialmente cuando queremos probar ideas o hipótesis sobre datos, o cuando queremos estimar rangos de valores para ciertas características de una población. Contenido¿Qué es la Distribución Ji al Cuadrado?La distribución ji al cuadrado se usa mucho en las pruebas de hipótesis. Estas pruebas nos ayudan a decidir si una idea o suposición sobre un grupo de datos es probable o no. También se usa para calcular intervalos de confianza, que son rangos de valores donde esperamos encontrar una característica de una población. ¿Para qué se usa?La distribución ji al cuadrado no se usa para describir fenómenos naturales directamente, como la altura de las personas o el tiempo que tarda algo en ocurrir. En cambio, es una herramienta matemática que aparece en muchas pruebas estadísticas, como:
También es una parte fundamental de otras distribuciones importantes en estadística, como la distribución t de Student y la distribución F, que se usan en análisis de datos más complejos. Su relación con la Distribución NormalLa razón principal por la que la distribución ji al cuadrado es tan útil es su conexión con la distribución normal. Cuando el número de datos en un estudio es grande, muchas pruebas estadísticas se comportan de manera similar a una distribución normal. La forma más sencilla de entender la distribución ji al cuadrado es pensar en ella como el cuadrado de una variable que sigue una distribución normal estándar. Si tienes una variable Así, si los valores extremos en una distribución normal tienen baja probabilidad, los valores extremos en una distribución ji al cuadrado también la tienen. Esto es clave para las pruebas de hipótesis, ya que los valores de baja probabilidad nos indican que algo inusual está ocurriendo. ¿Cómo se define la Distribución Ji al Cuadrado?Suma de Variables Normales EstándarImagina que tienes varias variables aleatorias independientes, digamos Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): Z_1, Z_2, \dots, Z_k , y cada una de ellas sigue una distribución normal estándar (con promedio 0 y varianza 1). Si sumas los cuadrados de estas variables, es decir, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): X = Z_1^2 + Z_2^2 + \dots + Z_k^2 , entonces la variable ¿Cómo se escribe?Cuando una variable aleatoria continua ¿Qué significa la función de densidad?La función de densidad de probabilidad nos dice qué tan probable es que una variable aleatoria tome un valor específico. Para la distribución ji al cuadrado, esta función tiene una forma matemática especial que depende de los grados de libertad ( A veces, los grados de libertad ( ¿Qué significa la función de distribución acumulada?La función de distribución acumulada nos dice la probabilidad de que una variable aleatoria tome un valor menor o igual a un número dado. Para la distribución ji al cuadrado, esta función también tiene una fórmula específica. Por ejemplo, si los grados de libertad son 2, la distribución ji al cuadrado se comporta como una distribución exponencial especial. Características ImportantesLa distribución ji al cuadrado tiene algunas características clave que nos ayudan a entenderla: Promedio (Media)El promedio o la media de una variable que sigue una distribución ji al cuadrado es igual a sus grados de libertad ( Variabilidad (Varianza)La varianza, que mide qué tan dispersos están los datos, es el doble de los grados de libertad ( Aplicaciones de la Distribución Ji al CuadradoLa distribución ji al cuadrado es una herramienta fundamental en la estadística. Sus usos más conocidos son:
También es crucial en el análisis de varianza, que se usa para comparar promedios de tres o más grupos, y en el análisis de regresión, que ayuda a entender la relación entre variables. Cómo usar la Tabla de Valores Ji al CuadradoCuando realizamos una prueba estadística que usa la distribución ji al cuadrado, obtenemos un valor. Para saber si este valor es "significativo" (es decir, si nos da suficiente evidencia para rechazar nuestra hipótesis inicial), usamos una tabla de valores ji al cuadrado o calculamos el "valor p". El valor p es la probabilidad de obtener un resultado tan extremo o más extremo que el que observamos, si nuestra hipótesis inicial fuera cierta. Un valor p bajo (generalmente menor a 0.05) nos indica que el resultado es estadísticamente significativo y que podemos rechazar la hipótesis inicial. La tabla siguiente muestra algunos valores de ji al cuadrado para diferentes grados de libertad y valores p. Por ejemplo, si tienes 7 grados de libertad y tu valor ji al cuadrado es 14.07, el valor p asociado es 0.05. Esto significa que hay un 5% de probabilidad de obtener un resultado así de extremo por casualidad.
Historia de la Distribución Ji al CuadradoEsta distribución fue descrita por primera vez por un científico alemán llamado Friedrich Robert Helmert entre 1875 y 1876. Él estudió cómo se distribuye la variabilidad de los datos en una muestra tomada de una población normal. Más tarde, el matemático inglés Karl Pearson la redescubrió de forma independiente en el año 1900. Pearson la usó para desarrollar su famosa prueba de ji-cuadrado de Pearson, que sirve para ver qué tan bien se ajustan los datos observados a lo que se espera. El nombre "ji al cuadrado" viene de la forma en que Pearson usaba la letra griega "ji" ( Véase también
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


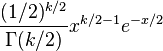 | cdf =
| cdf =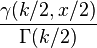 | mean =
| mean =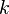 | median =aproximadamente
| median =aproximadamente 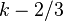 | mode =
| mode = si
si 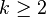 | variance =
| variance =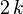 | skewness =
| skewness =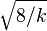 | kurtosis =
| kurtosis =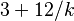 | entropy =
| entropy =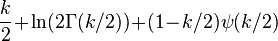 | mgf =
| mgf =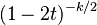 para
para 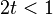 | char =
| char =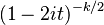 }} En el mundo de la
}} En el mundo de la 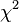 ) es una herramienta muy útil. Imagina que tienes varias variables aleatorias independientes que siguen una distribución normal estándar (como los resultados de un experimento que se agrupan alrededor de un promedio). Si elevas al cuadrado cada una de estas variables y luego las sumas, el resultado sigue una distribución ji al cuadrado.
) es una herramienta muy útil. Imagina que tienes varias variables aleatorias independientes que siguen una distribución normal estándar (como los resultados de un experimento que se agrupan alrededor de un promedio). Si elevas al cuadrado cada una de estas variables y luego las sumas, el resultado sigue una distribución ji al cuadrado.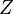 que es normal estándar (con promedio 0 y varianza 1), entonces Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): Z^2 sigue una distribución ji al cuadrado con 1 grado de libertad. Los "grados de libertad" indican cuántas variables normales independientes se sumaron al cuadrado para obtener la distribución.
que es normal estándar (con promedio 0 y varianza 1), entonces Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): Z^2 sigue una distribución ji al cuadrado con 1 grado de libertad. Los "grados de libertad" indican cuántas variables normales independientes se sumaron al cuadrado para obtener la distribución.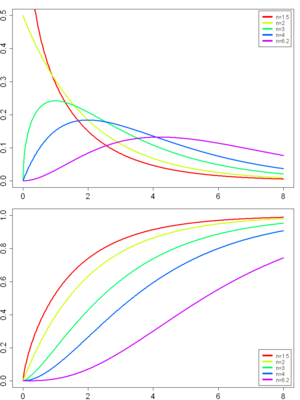
 tendrá una distribución ji al cuadrado con
tendrá una distribución ji al cuadrado con 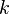 grados de libertad. El número
grados de libertad. El número 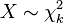 o
o 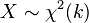 .
.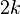 ). Si tiene 5 grados de libertad, su varianza será 10.
). Si tiene 5 grados de libertad, su varianza será 10.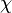 ) en sus fórmulas.
) en sus fórmulas. En inglés:
En inglés: