Intervalo de confianza para niños
En estadística, un intervalo de confianza es como un rango de números donde creemos que se encuentra el valor real de algo que estamos midiendo, pero que no podemos saber con exactitud. Imagina que quieres saber la altura promedio de todos los árboles en un bosque. No puedes medir cada árbol, así que tomas una muestra (mides algunos árboles). Con esa muestra, puedes calcular un intervalo de confianza.
Este intervalo nos dice que, con un cierto nivel de "confianza" (por ejemplo, 95%), el verdadero valor promedio de la altura de todos los árboles del bosque estará dentro de ese rango que calculaste. Si el nivel de confianza es del 95%, significa que si repitieras el proceso 100 veces, en 95 de esas veces el verdadero valor estaría dentro de tu intervalo. El 5% restante sería el "error" o la probabilidad de que el valor real no esté en tu intervalo.
Cuanto más amplio sea el intervalo, más seguros estaremos de que el valor real está dentro, pero la estimación será menos precisa. Si el intervalo es más pequeño, la estimación es más precisa, pero hay más riesgo de que el valor real esté fuera.
Contenido
¿Para qué sirve un intervalo de confianza?
Los intervalos de confianza son muy útiles en muchas áreas, como la ciencia, la medicina o la economía. Nos ayudan a tomar decisiones informadas cuando no podemos medir todo. Por ejemplo, si un médico prueba un nuevo medicamento, no puede dárselo a todas las personas del mundo. En su lugar, lo prueba en un grupo de pacientes y usa un intervalo de confianza para estimar cómo funcionaría en una población más grande.
¿Cómo se calcula un intervalo de confianza?
Para calcular un intervalo de confianza, necesitamos algunos datos de nuestra muestra, como el promedio de lo que medimos y qué tan dispersos están los datos. También necesitamos saber qué tan grande es nuestra muestra. Cuantos más datos tengamos en nuestra muestra, más preciso será el intervalo.
Ejemplos prácticos de intervalos de confianza
Estimando el peso de un producto
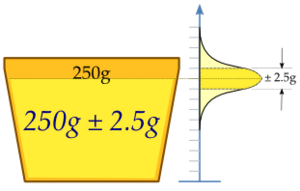
Imagina una máquina en una fábrica que llena tazas de helado. Se supone que cada taza debe tener 250 gramos. Pero, como todas las máquinas, no es perfecta y el peso puede variar un poco en cada taza. Para saber si la máquina está funcionando bien, un equipo de control de calidad toma una muestra de 25 tazas de helado y las pesa.
Supongamos que el peso promedio de esas 25 tazas es de 250.2 gramos. Este es solo el promedio de la muestra, no el peso exacto de todas las tazas que la máquina produce. Para saber si la máquina está bien ajustada, necesitamos un intervalo de confianza.
Si sabemos que la máquina normalmente tiene una variación de 2.5 gramos (esto se llama "desviación estándar"), podemos calcular un intervalo de confianza. Para un nivel de confianza del 95%, el cálculo nos diría que el peso promedio real de todas las tazas que produce la máquina está entre 249.22 gramos y 251.18 gramos.
Como el peso deseado de 250 gramos está dentro de este intervalo (entre 249.22 y 251.18), podemos decir que la máquina está funcionando correctamente. Si el 250 no estuviera en el intervalo, significaría que la máquina necesita ser ajustada.
¿Qué significa el nivel de confianza?
Cuando decimos que tenemos un "nivel de confianza" del 95%, significa que si repitiéramos este experimento de pesar 25 tazas muchas veces, el 95% de los intervalos de confianza que calcularíamos incluirían el verdadero peso promedio de todas las tazas. Sin embargo, el 5% de las veces, el intervalo que calculamos no incluiría el verdadero peso. No sabemos si el intervalo que calculamos en un momento dado es uno de los que sí lo contiene o uno de los que no. Por eso, hablamos de "nivel de confianza" y no de "probabilidad" de que el valor esté en un intervalo específico.
Galería de imágenes
-
Esta imagen muestra cómo se distribuyen los datos alrededor de un promedio en una curva.
-
El segmento vertical representa 50 realizaciones de un intervalo de confianza para un valor promedio.
Ver también
- Estimación estadística
- Tamaño de la muestra
Véase también
En inglés: Confidence interval Facts for Kids
