Distribución geométrica para niños
Datos para niños Geométrica |
||
|---|---|---|
| Parámetros | 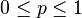 |
|
| Dominio | Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x\in\{1,2,\dots\} | |
| Función de densidad (pdf) | Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): p(1-p)^{x-1} | |
| Función de distribución (cdf) | Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 1-(1-p)^{x} | |
| Media |  |
|
| Moda | 0 | |
| Varianza | 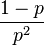 |
|
| Coeficiente de simetría |
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{2-p}{\sqrt{1-p</td></tr><tr><td class="noprint" colspan="3" style="text-align:left;"></td></tr></table><!--IB_END--> |kurtosis= En el mundo de la teoría de probabilidad y la estadística, la distribución geométrica es una herramienta matemática muy útil. Nos ayuda a calcular la probabilidad de cuántos intentos necesitamos para conseguir algo por primera vez. Imagina que estás lanzando una moneda hasta que salga "cara". La distribución geométrica te diría cuántos lanzamientos es probable que necesites. Existen dos formas principales de entenderla:
Contenido¿Cómo Funciona la Distribución Geométrica?¿Qué es una Variable Aleatoria Geométrica?Una variable aleatoria es un valor que puede cambiar en un experimento. Si una variable Calculando la Probabilidad de ÉxitoSi queremos saber la probabilidad de que el primer éxito ocurra exactamente en el intento número
Aquí, Por ejemplo, si la probabilidad de éxito (
Esto significa que hay un 12.8% de probabilidad de que el primer éxito sea en el tercer intento. ¿Cómo se Acumulan las Probabilidades?La función de distribución nos dice la probabilidad de que el primer éxito ocurra en el intento Se calcula sumando las probabilidades de que el éxito ocurra en el primer intento, en el segundo, y así sucesivamente, hasta el intento
Características Importantes¿Cuál es el Número Promedio de Intentos?La media (o promedio) de una distribución geométrica nos dice cuántos intentos esperamos necesitar para conseguir el primer éxito. Se calcula de forma sencilla: Si la probabilidad de éxito ( ¿Qué Tan Variados Son los Resultados?La varianza nos indica qué tan dispersos o variados son los resultados alrededor del promedio. Una varianza alta significa que los resultados pueden estar muy lejos del promedio, mientras que una baja indica que están más cerca. Para la distribución geométrica, la varianza se calcula así: La Propiedad de "Pérdida de Memoria"Una característica muy especial de la distribución geométrica es su "pérdida de memoria". Esto significa que el pasado no afecta el futuro. Imagina que estás lanzando una moneda para obtener "cara". Si ya has lanzado la moneda 10 veces y no ha salido "cara", la probabilidad de que salga "cara" en el siguiente lanzamiento sigue siendo la misma que al principio. La moneda no "recuerda" los lanzamientos anteriores. En términos matemáticos, esto se expresa como:
Esto significa que la probabilidad de necesitar La distribución geométrica es la única distribución discreta (que cuenta cosas) que tiene esta propiedad. Otras Distribuciones Relacionadas
Véase también
|
|


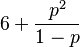 |entropy=
|entropy=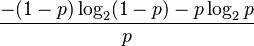 |mgf=Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{pe^t}{1-(1-p)e^t} }}
|mgf=Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{pe^t}{1-(1-p)e^t} }} sigue una distribución geométrica con un parámetro
sigue una distribución geométrica con un parámetro 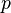 (que es la probabilidad de éxito en cada intento), lo escribimos como
(que es la probabilidad de éxito en cada intento), lo escribimos como 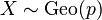 . El valor de
. El valor de  (contando todos los intentos), usamos esta fórmula:
(contando todos los intentos), usamos esta fórmula: es la probabilidad de fracaso. La parte Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (1-p)^{x-1} significa que hubo
es la probabilidad de fracaso. La parte Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (1-p)^{x-1} significa que hubo  fracasos antes del éxito final.
fracasos antes del éxito final. ):
):![\operatorname{E}[X]=\frac{1}{p}](/images/math/8/7/4/8740ee5e4fb40197074b3f823f441fd0.png)
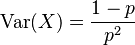
![\operatorname{P}[X > m+n | X>m]=\operatorname{P}[X>n]](/images/math/e/e/e/eeeabd8c880cc625160682a54725d2b6.png) .
. intentos adicionales, dado que ya fallaste
intentos adicionales, dado que ya fallaste 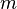 veces, es la misma que la probabilidad de necesitar
veces, es la misma que la probabilidad de necesitar  En inglés:
En inglés: