Cálculo mental para niños

El cálculo mental es la habilidad de resolver problemas de matemáticas usando solo tu cerebro, sin la ayuda de calculadoras, lápiz y papel, o incluso tus dedos. A menudo, el cálculo mental usa trucos especiales para diferentes tipos de problemas.

Las personas que son muy buenas haciendo cálculos mentales se llaman calculistas mentales. Algunos de ellos pueden resolver operaciones muy difíciles, como multiplicar números grandes, solo con su mente. Sin embargo, los mejores matemáticos no siempre son los mejores calculistas. Tampoco los grandes calculistas son los que tienen mejor memoria, porque las técnicas para calcular y para memorizar son diferentes. Los campeones mundiales de cálculo y de memoria suelen ser personas distintas.

Practicar el cálculo mental ayuda a los estudiantes a pensar de diferentes maneras. Algunos de sus beneficios son: mejorar el sentido numérico (entender mejor los números) y desarrollar habilidades como la atención y la concentración. También puede hacer que te gusten más las matemáticas. Para aprenderlo, es bueno descubrir reglas que te ayuden a recordar cosas (reglas mnemotécnicas).

Cálculo mental. En la escuela pública S. A. Rachinski, cuadro de Nikolái Bogdanov-Belski de 1895 en el que unos niños tratan de calcular mentalmente el resultado de la expresión en la pizarra, .

Estrategias para el Cálculo Mental

Cómo Sumar y Restar Mentalmente

Si al sumar no hay "llevadas" (es decir, si ninguna suma de dígitos es mayor que 9), puedes sumar directamente. Lo mismo ocurre con las restas.

Si hay llevadas, necesitas pensar en los números de otra forma. A veces, una suma de dos números se puede convertir en una suma más sencilla con más partes. Lo mismo pasa con las restas. Algunos calculistas sugieren sumar siempre de izquierda a derecha, incluso con llevadas.

Ejemplos:

• Calcular 456 + 155:

• 456 + 155 = 556 + 55 = 606 + 5 = 611 (sumando de izquierda a derecha).

• Calcular 876 - 98:

• 876 - 98 = 876 - (100 - 2) = 876 - 100 + 2 = 776 + 2 = 778 (usando un número cercano que sea fácil de restar, como 100).

Multiplicaciones y Divisiones Rápidas

Duplicar y Reducir a la Mitad

Multiplicar por 2 es como sumar el número a sí mismo. Duplicar y reducir a la mitad eran técnicas muy importantes en las matemáticas egipcias.

Ejemplo: Multiplicar 173 × 16:

• Puedes duplicar el primer número y reducir a la mitad el segundo: 173 × 16 = 346 × 8 = 692 × 4 = 1384 × 2 = 2768.

Este método también sirve para multiplicar por números que son potencias de 2 y 5. Multiplicar por 5 es como calcular la mitad del número y luego multiplicarlo por 10.

Ejemplo: Multiplicar 376 × 125:

• Como 125 es 1000 dividido por 8 (10³/2³), puedes añadir tres ceros y dividir tres veces por 2.
• 376 × 125 = 376000 / 8 = 188000 / 4 = 94000 / 2 = 47000.

Es útil conocer algunas potencias de 2 y 5 para hacer estas operaciones con facilidad.

Multiplicar por Números Cercanos a Potencias de 10

Multiplicar por 9, 11, 99, 101, etc., es decir, por un número cercano a 10, 100, 1000, puede hacerse mentalmente. Por ejemplo, 28 × 99 es lo mismo que 28 × (100 - 1).

Ejemplo: Multiplicar 28 × 99:

• 28 × 99 = 28 × (100 - 1) = 2800 - 28 = 2772.

Multiplicar por 11 es especialmente fácil:

• Para 12345 × 11:

• Escribe el último dígito (5).
• Suma los dígitos de dos en dos de derecha a izquierda (5+4=9, 4+3=7, 3+2=5, 2+1=3).
• Escribe el primer dígito (1).
• El resultado es 135795.

• Para 8946 × 11:

• Último dígito (6).
• 6+4=10 (escribe 0, lleva 1).
• 4+9+1 (llevada) = 14 (escribe 4, lleva 1).
• 9+8+1 (llevada) = 18 (escribe 8, lleva 1).
• Primer dígito 8+1 (llevada) = 9.
• El resultado es 98406.

Multiplicación por 37

Para multiplicar por 37, puedes recordar que 37 × 3 = 111 y 37 × 27 = 999. El truco es dividir el otro número entre 3. Ejemplo: 37 × 94

1. Divide 94 entre 3: 94 : 3 = 31 con un resto de 1.
2. Multiplica 111 por 31: 111 × 31 = 3441.
3. Como el resto era 1, suma 37 al resultado: 3441 + 37 = 3478.

Igualdades Notables y Cuadrados

Las igualdades notables son fórmulas que te ayudan a calcular más rápido:

1. (a + b)² = a² + 2ab + b²
2. (a - b)² = a² - 2ab + b²
3. (a + b) (a - b) = a² - b²

Calcular el Cuadrado de un Número de Dos Cifras

Puedes usar las dos primeras fórmulas para calcular el cuadrado de un número. Ejemplo: Calcular 52²

• 52 = 50 + 2. Usa (a + b)² con a=50 y b=2.
• (50 + 2)² = 50² + 2 × 2 × 50 + 2² = 2500 + 200 + 4 = 2704.

Ejemplo: Calcular 95²

• 95 = 90 + 5.
• (90 + 5)² = 90² + 2 × 5 × 90 + 5² = 8100 + 900 + 25 = 9025.

Multiplicar Números a la Misma Distancia de un Número Conocido

Si quieres multiplicar 58 × 62, puedes usar el 60 como referencia, porque ambos están a 2 unidades de 60. Usa la tercera fórmula: (a + b) (a - b) = a² - b².

• (60 + 2) (60 - 2) = 60² - 2² = 3600 - 4 = 3596.

Ejemplo: 95 × 105

• (100 - 5) (100 + 5) = 100² - 5² = 10000 - 25 = 9975.

Cuadrado de un Número Terminado en 5

Para calcular el cuadrado de un número que termina en 5, como 65², puedes usar un truco. Multiplica el primer dígito (6) por el siguiente número (7), y luego añade 25 al final.

• 65²: 6 × 7 = 42. Añade 25. Resultado: 4225.

Ejemplo: 35 × 35

• 3 × 4 = 12. Añade 25. Resultado: 1225.

Raíces Cuadradas y Cúbicas

Aproximar Raíces Cuadradas

Puedes estimar la raíz cuadrada de un número usando una fórmula. Cuanto más cerca esté el cuadrado conocido del número que buscas, más precisa será tu estimación.

Fórmula:

Ejemplo: Estimar la raíz cuadrada de 15. Sabemos que 4² = 16.

La raíz cuadrada real de 15 es aproximadamente 3.872983.

Extraer Raíces Cúbicas

Una tarea común es encontrar la raíz cúbica de un número que es el resultado de multiplicar un número por sí mismo tres veces. Por ejemplo, si te dan 74088, ¿qué número multiplicado por sí mismo tres veces da 74088? La respuesta es 42, porque 42³ = 74088.

Para esto, necesitas memorizar los cubos de los números del 1 al 10:

Hay un patrón en el último dígito de los cubos:

• Si el cubo termina en 0, su raíz cúbica termina en 0.
• Si el cubo termina en 1, su raíz cúbica termina en 1.
• Si el cubo termina en 2, su raíz cúbica termina en 8.
• Si el cubo termina en 3, su raíz cúbica termina en 7.
• Si el cubo termina en 4, su raíz cúbica termina en 4.
• Si el cubo termina en 5, su raíz cúbica termina en 5.
• Si el cubo termina en 6, su raíz cúbica termina en 6.
• Si el cubo termina en 7, su raíz cúbica termina en 3.
• Si el cubo termina en 8, su raíz cúbica termina en 2.
• Si el cubo termina en 9, su raíz cúbica termina en 9.

Para encontrar la raíz cúbica de un número de dos dígitos, sigue estos pasos: Ejemplo: Encontrar la raíz cúbica de 29791.

1. Mira el último dígito del número (1). Según la tabla, la raíz cúbica debe terminar en 1.
2. Quita los últimos tres dígitos del número (29791 → 29).
3. Busca el cubo más grande que sea menor o igual a 29.

• 1³ = 1, 2³ = 8, 3³ = 27, 4³ = 64.
• El cubo más grande que no se pasa de 29 es 27 (que es 3³). Así que el primer dígito de la raíz cúbica es 3.

1. La raíz cúbica de 29791 es 31.

Otro ejemplo: Hallar la raíz cúbica de 456533.

• El número termina en 3, así que la raíz cúbica termina en 7.
• Quita los últimos tres dígitos: 456.
• Busca el cubo más grande que no se pase de 456.

• 7³ = 343, 8³ = 512.
• El cubo más grande que no se pasa de 456 es 343 (que es 7³). Así que el primer dígito es 7.

• La raíz cúbica de 456533 es 77.

Calcular Logaritmos (Base 10)

Para estimar el logaritmo común (en base 10), necesitas saber algunas propiedades y memorizar algunos logaritmos básicos:

• log(1) = 0
• log(2) es aproximadamente 0.30
• log(3) es aproximadamente 0.48
• log(10) = 1
• Si un número es mayor que otro, su logaritmo también será mayor.

Con esto, puedes calcular otros logaritmos:

• log(4) = log(2 × 2) = log(2) + log(2) = 0.30 + 0.30 = 0.60
• log(5) = log(10 : 2) = log(10) - log(2) = 1 - 0.30 = 0.70

Para aproximar el logaritmo de un número, primero escríbelo en notación científica. Por ejemplo, 45 es 4.5 × 10¹. Luego, estima el logaritmo de la primera parte (4.5). Como 4.5 está a la mitad entre 4 y 5, su logaritmo (log(4.5)) estará a la mitad entre log(4) (0.60) y log(5) (0.70), es decir, aproximadamente 0.65. Finalmente, suma el exponente de 10. Para 45, log(45) es aproximadamente 0.65 + 1 = 1.65.

Cómo Verificar tus Resultados

Hay varias maneras de comprobar si tu cálculo mental es correcto:

• Orden de magnitud: Si multiplicas dos números menores de 100 y el resultado es mayor de 10,000, algo anda mal. El número de cifras del resultado debe ser similar a la suma de las cifras de los números que multiplicaste.
• Última cifra: Comprueba que el último dígito de tu resultado sea correcto. Por ejemplo, 73 × 64 debe terminar en 2, porque 3 × 4 = 12.
• Prueba del nueve: Suma los dígitos de cada número y del resultado hasta que te quede un solo dígito. Luego, multiplica los dígitos de los números originales y compara con el dígito del resultado.

• Ejemplo: Si calculaste 73 × 64 = 4662.
• 7 + 3 = 10 → 1 + 0 = 1
• 6 + 4 = 10 → 1 + 0 = 1
• 4 + 6 + 6 + 2 = 18 → 1 + 8 = 9
• Multiplica los resultados: 1 × 1 = 1.
• Como 1 no es igual a 9, el resultado 4662 es incorrecto. (El resultado correcto es 4672).

El Cálculo Mental y la Mente

Hacer ejercicio físico antes de una tarea mental, como el cálculo, puede mejorar tu rendimiento. Sin embargo, si el ejercicio es demasiado intenso, puede tener el efecto contrario y disminuir tu precisión. Los estudios han mostrado que la actividad cerebral (medida con un electroencefalograma o EEG) puede ayudar a entender cuánto esfuerzo mental se está usando.

Competiciones de Cálculo Mental

Existen varias competiciones donde las personas demuestran sus habilidades de cálculo mental.

Campeonato Mundial de Cálculos Mentales

El primer Campeonato Mundial de Cálculos Mentales se realizó en 1997. Se celebra cada año y tiene diferentes pruebas, como sumar diez números de diez dígitos, multiplicar números grandes, calcular raíces cuadradas y cúbicas, y determinar el día de la semana para fechas específicas.

Copa del Mundo de Cálculo Mental

La Copa del Mundo de Cálculo Mental comenzó en 2004 y se celebra cada dos años. Incluye pruebas similares al Campeonato Mundial, como sumas, multiplicaciones, raíces cuadradas y cúbicas, y cálculo de fechas.

Memoriad - Olimpiadas Mundiales de Memoria, Cálculo Mental y Lectura Veloz

El Memoriad es una competición única que combina cálculo mental, memoria y lectura rápida. Se lleva a cabo cada cuatro años, coincidiendo con los Juegos Olímpicos. El primer Memoriad fue en Estambul, Turquía, en 2008. La segunda edición fue en Antalya, Turquía, en 2012, con 89 participantes de 20 países. Se entregaron premios en 10 categorías, de las cuales 5 eran de cálculo mental.

Galería de imágenes

• 

  Cálculo mental. En la escuela pública S. A. Rachinski, cuadro de Nikolái Bogdanov-Belski de 1895 en el que unos niños tratan de calcular mentalmente el resultado de la expresión en la pizarra, .

Véase también

En inglés: Mental calculation Facts for Kids

• Calculadora humana
• Calculista mental
• Ábaco
• Ábaco mental
• Mnemotecnia
• Regla del fin del mundo para el cálculo del día de la semana
• Soroban
• Método Trachtenberg
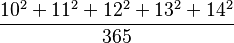