Axioma de elección para niños

Ejemplo del axioma de elección.

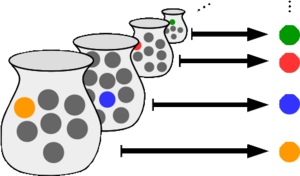
En el mundo de las matemáticas, el axioma de elección es una regla fundamental que nos dice algo importante sobre cómo podemos trabajar con colecciones de cosas. Imagina que tienes muchas "cajas", y cada caja tiene al menos un objeto dentro. El axioma de elección dice que siempre es posible "elegir" un objeto de cada una de esas cajas, sin importar cuántas cajas haya.

Si tienes un número limitado de cajas (un grupo "finito"), es fácil entender cómo elegir un objeto de cada una. Simplemente vas de caja en caja y escoges un objeto. Pero, ¿qué pasa si tienes un número infinito de cajas? Y, ¿qué pasa si no hay una regla clara para elegir un objeto de cada caja? Por ejemplo, si una caja contiene todos los números entre 0 y 1, ¿cuál eliges? No hay un "primer" número en esa colección. En estos casos, el axioma de elección es muy útil.

Este axioma fue propuesto en 1904 por un matemático llamado Ernst Zermelo. Lo usó para demostrar que cualquier colección de elementos puede ser "bien ordenada". Aunque al principio causó algo de debate entre los matemáticos, hoy en día la mayoría lo usa sin problemas. Sin embargo, algunos matemáticos, especialmente en la teoría de conjuntos, prefieren no usarlo o exploran qué pasaría si no fuera cierto.

¿Qué dice el axioma de elección?

Para entenderlo mejor, piensa en una "función de elección". Una función de elección es como un ayudante que, para cada caja que le das (siempre que la caja no esté vacía), te devuelve uno de los objetos que están dentro de esa caja.

El axioma de elección, de forma sencilla, dice que:

• Si tienes una colección de cajas, y ninguna de ellas está vacía, entonces siempre existe un ayudante (una función de elección) que puede elegir un objeto de cada caja.

También se puede expresar de otras maneras que significan lo mismo:

• Toda colección de conjuntos que no están vacíos tiene una función de elección.
• Si multiplicas todas las colecciones de objetos (lo que se llama "producto cartesiano"), el resultado no estará vacío.
• Para cualquier colección de objetos, puedes encontrar una función de elección para todas sus subcolecciones que no estén vacías.
• Si tienes una colección de cajas que no están vacías y no comparten objetos entre sí, siempre puedes encontrar una colección de objetos que contenga exactamente un objeto de cada una de esas cajas.

Por el contrario, si el axioma de elección no fuera cierto, significaría que existe al menos una colección de cajas no vacías de la que no se podría elegir un objeto de cada una.

¿Para qué se usa?

Durante mucho tiempo, los matemáticos usaron el axioma de elección sin darse cuenta. Simplemente asumían que si tenían una colección de conjuntos no vacíos, podían elegir un elemento de cada uno. Pero fue Zermelo quien señaló que, en muchos casos, no se puede demostrar que esa elección sea posible sin este axioma.

Como mencionamos, si tienes un número finito de cajas, no necesitas el axioma de elección. Es como si tuvieras 5 cajas de juguetes; puedes ir una por una y sacar un juguete de cada una. Esto es algo que se puede hacer paso a paso.

La dificultad surge con las colecciones infinitas. Imagina que tienes una caja para cada número real entre 0 y 1. ¿Cómo eliges un número de cada una? No puedes ir "uno por uno" porque nunca terminarías. Además, no hay una regla sencilla como "elige el número más pequeño", porque algunos conjuntos, como el intervalo (0, 1), no tienen un número más pequeño.

A veces, se podría pensar en "ordenar" los elementos de una manera especial para poder elegir el primero. Pero para poder ordenar bien algunos conjuntos infinitos, ¡necesitas el axioma de elección! Es como un círculo: para resolver un problema, necesitas el axioma, y el axioma te ayuda a resolver ese problema.

Una cosa importante es que las demostraciones que usan el axioma de elección no te dicen exactamente "cuál" es el objeto elegido. Solo te dicen que "existe" un objeto. Por ejemplo, el axioma puede decir que existe una forma de ordenar los números reales, pero no te dice cómo es ese orden. Esto es algo que a algunos matemáticos no les gusta, especialmente a los "constructivistas", que creen que si algo existe, deberíamos poder encontrarlo de forma explícita.

¿Es independiente de otras reglas?

Gracias al trabajo de matemáticos como Kurt Gödel y Paul Cohen, sabemos que el axioma de elección es "independiente" de las otras reglas básicas de la teoría de conjuntos (conocidas como ZF). Esto significa que no se puede demostrar que el axioma de elección sea verdadero ni falso usando solo esas otras reglas. Es como si fuera una regla extra que puedes decidir añadir o no.

Si decides usarlo, no te llevará a contradicciones que no existieran antes. Muchos matemáticos lo usan porque es muy útil y permite demostrar muchas cosas que de otra manera serían imposibles.

Sin embargo, el axioma de elección puede llevar a resultados que parecen muy extraños o "contra-intuitivos". Un ejemplo famoso es la paradoja de Banach-Tarski. Esta paradoja dice que, en teoría, podrías dividir una esfera en varias partes y, solo moviéndolas y girándolas, se pueden formar dos esferas del mismo tamaño que la original. Es importante recordar que esto es una idea matemática, no algo que se pueda hacer con una esfera física en la vida real. La demostración solo dice que "existe" esa posibilidad, no cómo hacerlo.

Por otro lado, si negamos el axioma de elección, también obtenemos resultados extraños. Por ejemplo, podría haber conjuntos de los que no se puede decir cuál es más grande que el otro.

Reglas relacionadas

Existen otras reglas que son similares o más fuertes que el axioma de elección:

• El axioma de elección numerable es una versión más suave. Dice que si tienes una colección de conjuntos que puedes contar (como los números naturales), entonces sí puedes elegir un elemento de cada uno. Esto es suficiente para muchas demostraciones en matemáticas.
• El axioma de elección dependiente es otra versión que también es más suave.

¿Qué resultados necesitan el axioma de elección?

Muchos resultados importantes en matemáticas necesitan el axioma de elección para ser demostrados. Aquí hay algunos ejemplos de cosas que no se pueden probar sin él, pero sí con él:

• Cualquier unión de conjuntos contables (que se pueden numerar) es también contable.
• Si un conjunto es infinito, puedes encontrar una forma de relacionarlo con los números naturales.
• Existen subconjuntos de los números reales que no se pueden "medir" de la forma usual.
• La paradoja de Banach-Tarski (la de la esfera que se duplica).
• Todo espacio vectorial (un tipo de estructura matemática) tiene una "base" (un conjunto de elementos que permiten construir todos los demás).
• Todo cuerpo (otro tipo de estructura matemática) tiene una "clausura algebraica" (una extensión donde todas las ecuaciones tienen solución).
• Cualquier conjunto puede ser "ordenado" de forma lineal.

¿Qué pasa si no se usa el axioma de elección?

Si no se usa el axioma de elección, algunas cosas que damos por sentadas en matemáticas podrían no ser ciertas. Por ejemplo, en algunos modelos de la teoría de conjuntos sin el axioma de elección, podría haber:

• Funciones que no son continuas de la forma esperada.
• El conjunto de los números reales podría ser una unión contable de conjuntos contables.
• Espacios vectoriales sin base.
• Espacios vectoriales con dos bases de diferente tamaño.
• Todos los subconjuntos de los números reales podrían ser medibles, lo que eliminaría paradojas como la de Banach-Tarski.

Galería de imágenes

• 

  Ejemplo del axioma de elección.

Véase también

En inglés: Axiom of choice Facts for Kids