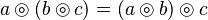Asociatividad (álgebra) para niños
La asociatividad es una propiedad muy importante en las matemáticas y la lógica. Imagina que tienes tres o más números o elementos y quieres combinarlos usando una operación, como la suma o la multiplicación. Si el orden en que agrupas esos elementos no cambia el resultado final, entonces esa operación es asociativa.
Por ejemplo, si tienes los números 2, 3 y 4 y quieres sumarlos, puedes hacer:
- (2 + 3) + 4 = 5 + 4 = 9
- 2 + (3 + 4) = 2 + 7 = 9
Como ves, el resultado es el mismo (9) sin importar cómo agrupamos los números con los paréntesis. Esto significa que la suma es una operación asociativa. Lo mismo ocurre con la multiplicación.
Es importante no confundir la asociatividad con la conmutatividad. La conmutatividad se refiere a si puedes cambiar el orden de los elementos sin alterar el resultado. Por ejemplo, 2 + 3 es lo mismo que 3 + 2. La suma es conmutativa y asociativa. Sin embargo, algunas operaciones pueden ser asociativas pero no conmutativas, como la multiplicación de matrices.
Contenido
¿Qué significa la propiedad asociativa?
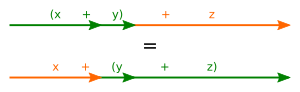
La propiedad asociativa se cumple cuando, al realizar una operación con tres o más elementos, el resultado no cambia aunque reorganices los paréntesis. Lo importante es que los elementos mantengan su orden original.
Por ejemplo, para una operación que llamaremos  , si tienes los elementos a, b y c, la asociatividad significa que:
, si tienes los elementos a, b y c, la asociatividad significa que:
Esto es muy útil porque nos permite escribir expresiones largas sin preocuparnos por dónde ponemos los paréntesis, siempre que la operación sea asociativa.
Ejemplos de operaciones asociativas
- Suma de números: Como vimos, (2 + 3) + 4 es igual a 2 + (3 + 4).
- Multiplicación de números: (2 × 3) × 4 es igual a 2 × (3 × 4). Ambos dan 24.
- Concatenación de textos: Si unes las palabras "hola", " " y "mundo", puedes hacer ("hola" + " ") + "mundo" o "hola" + (" " + "mundo"). En ambos casos, el resultado es "hola mundo".
- Máximo Común Divisor (MCD) y Mínimo Común Múltiplo (MCM): Estas operaciones también son asociativas.
- Unión e Intersección de conjuntos: Si tienes conjuntos A, B y C, la unión (A ∪ B) ∪ C es igual a A ∪ (B ∪ C). Lo mismo ocurre con la intersección.
- Composición de funciones: Cuando combinas varias funciones, el orden en que las agrupas no cambia el resultado final.
Operaciones que no son asociativas
No todas las operaciones cumplen la propiedad asociativa. Cuando una operación no es asociativa, el orden en que agrupas los elementos sí importa y puede cambiar el resultado.
Ejemplos de operaciones no asociativas
- Resta:
- 5 - (3 - 2) = 5 - 1 = 4
- (5 - 3) - 2 = 2 - 2 = 0
Como 4 no es igual a 0, la resta no es asociativa.
- División:
- (4 : 2) : 2 = 2 : 2 = 1
- 4 : (2 : 2) = 4 : 1 = 4
Como 1 no es igual a 4, la división no es asociativa.
- Exponenciación (potencias):
- 2(23) = 28 = 256
- (22)3 = 43 = 64
Como 256 no es igual a 64, la exponenciación no es asociativa.
Asociatividad en la informática
En la informática, especialmente cuando se trabaja con números de coma flotante (números con decimales), la suma y la multiplicación pueden no ser perfectamente asociativas. Esto se debe a los errores de redondeo que ocurren cuando los ordenadores manejan números muy grandes o muy pequeños. Por eso, los programadores a veces usan métodos especiales para minimizar estos errores.
Asociatividad en la lógica
En la lógica proposicional, la asociatividad es una regla que permite mover los paréntesis en expresiones lógicas sin cambiar su significado. Esto es muy útil en las demostraciones lógicas.
Por ejemplo, para las operaciones lógicas "o" (disyunción) y "y" (conjunción):
- Asociatividad de la disyunción (o):
- Asociatividad de la conjunción (y):
Esto significa que no importa cómo agrupemos las afirmaciones con "o" o "y", el resultado lógico será el mismo.
Galería de imágenes
Véase también
 En inglés: Associativity Facts for Kids
En inglés: Associativity Facts for Kids