Aplicación lineal para niños
En matemáticas, una aplicación lineal (también llamada transformación lineal o función lineal) es un tipo especial de función que conecta dos espacios vectoriales. Imagina que los espacios vectoriales son como "mundos" donde viven "flechas" (vectores) que puedes sumar o multiplicar por números. Una aplicación lineal es una regla que toma una flecha de un mundo y la convierte en una flecha del otro mundo, pero de una manera muy ordenada: mantiene las relaciones de suma y multiplicación.
Esto significa que si sumas dos flechas en el primer mundo y luego aplicas la regla, el resultado es el mismo que si aplicaras la regla a cada flecha por separado y luego sumaras los resultados en el segundo mundo. Lo mismo ocurre si multiplicas una flecha por un número.
Plantilla:Ficha de concepto
Contenido
- ¿Qué es una Aplicación Lineal?
- ¿Cómo se define una Aplicación Lineal?
- Ejemplos Sencillos de Aplicaciones Lineales
- Propiedades Importantes de las Transformaciones Lineales
- ¿Cómo crear nuevas Transformaciones Lineales?
- Teoremas Clave sobre Transformaciones Lineales
- Tipos de Transformaciones Lineales
- La Matriz Asociada a una Transformación Lineal
- Galería de imágenes
- Véase también
¿Qué es una Aplicación Lineal?
Una aplicación lineal es una función que toma elementos de un espacio vectorial (llamado dominio) y los transforma en elementos de otro espacio vectorial (llamado codominio), siguiendo dos reglas muy importantes. Estas reglas aseguran que la función se comporte de manera "lineal", es decir, sin curvas ni cambios inesperados.
¿Cómo se define una Aplicación Lineal?
Para que una función 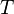 sea una aplicación lineal entre dos espacios vectoriales
sea una aplicación lineal entre dos espacios vectoriales  y
y 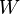 (que usan el mismo tipo de números, como los números reales), debe cumplir estas dos condiciones para cualquier par de flechas
(que usan el mismo tipo de números, como los números reales), debe cumplir estas dos condiciones para cualquier par de flechas 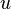 y
y 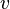 de
de  , y para cualquier número
, y para cualquier número 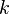 :
:
- 1. Suma de flechas: Si sumas dos flechas y luego aplicas
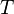 , es lo mismo que aplicar
, es lo mismo que aplicar 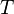 a cada flecha por separado y luego sumar los resultados:
a cada flecha por separado y luego sumar los resultados:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): T(u+v) = T(u) + T(v)
- 2. Multiplicación por un número: Si multiplicas una flecha por un número y luego aplicas
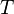 , es lo mismo que aplicar
, es lo mismo que aplicar 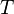 a la flecha y luego multiplicar el resultado por el mismo número:
a la flecha y luego multiplicar el resultado por el mismo número:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): T(ku) = kT(u)
Estas dos reglas juntas se conocen como el "principio de superposición".
Ejemplos Sencillos de Aplicaciones Lineales
Para entender mejor, veamos algunos ejemplos de funciones que sí son aplicaciones lineales:
Identidad y Homotecias
- La función identidad: Imagina una función que no cambia nada. Si tienes una flecha
 , la función Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): T(x) = x simplemente devuelve la misma flecha. Esta es una aplicación lineal porque cumple las dos reglas.
, la función Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): T(x) = x simplemente devuelve la misma flecha. Esta es una aplicación lineal porque cumple las dos reglas. - Las homotecias: Son funciones que "estiran" o "encogen" las flechas. Por ejemplo, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): T(x) = kx , donde
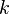 es un número. Si
es un número. Si 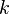 es mayor que 1, las flechas se hacen más largas (dilatación). Si
es mayor que 1, las flechas se hacen más largas (dilatación). Si 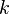 es menor que 1 (pero positivo), se hacen más cortas (contracción).
es menor que 1 (pero positivo), se hacen más cortas (contracción).
- Multiplicación por una matriz: Si tienes una matriz
 , la función que toma una flecha
, la función que toma una flecha  y la multiplica por
y la multiplica por  (
(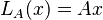 ) es una aplicación lineal. Esto es muy útil porque muchas transformaciones lineales se pueden representar con matrices.
) es una aplicación lineal. Esto es muy útil porque muchas transformaciones lineales se pueden representar con matrices.
Propiedades Importantes de las Transformaciones Lineales
Las aplicaciones lineales tienen características especiales que las hacen muy útiles en matemáticas y otras ciencias.
El Núcleo y la Imagen
Cuando trabajamos con una aplicación lineal 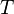 que va de un espacio
que va de un espacio  a un espacio
a un espacio 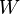 , podemos definir dos conjuntos importantes:
, podemos definir dos conjuntos importantes:
- El Núcleo (ker): Es el conjunto de todas las flechas en el espacio original
 que, al aplicarles
que, al aplicarles 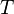 , se convierten en la flecha "cero" del espacio
, se convierten en la flecha "cero" del espacio 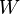 . Es como si estas flechas "desaparecieran" o se encogieran hasta un punto.
. Es como si estas flechas "desaparecieran" o se encogieran hasta un punto.
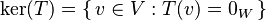 El núcleo siempre es un subespacio vectorial del espacio original. Esto significa que si tomas dos flechas del núcleo y las sumas, el resultado también estará en el núcleo. Lo mismo si multiplicas una flecha del núcleo por un número.
El núcleo siempre es un subespacio vectorial del espacio original. Esto significa que si tomas dos flechas del núcleo y las sumas, el resultado también estará en el núcleo. Lo mismo si multiplicas una flecha del núcleo por un número.
- La Imagen (im): Es el conjunto de todas las flechas en el espacio de llegada
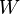 que son el resultado de aplicar
que son el resultado de aplicar 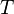 a alguna flecha del espacio original
a alguna flecha del espacio original  . Es como ver todas las posibles "salidas" de la función.
. Es como ver todas las posibles "salidas" de la función.
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \operatorname{im}(T)=\{\,w\in W: \exists v\in V:T(v)=w\,\} La imagen también es un subespacio vectorial del espacio de llegada.
La nulidad de una transformación lineal es la "dimensión" (cuántas flechas independientes la forman) de su núcleo. El rango es la dimensión de su imagen.
¿Cómo crear nuevas Transformaciones Lineales?
Podemos combinar aplicaciones lineales para formar nuevas:
- Suma de aplicaciones lineales: Si tienes dos aplicaciones lineales
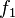 y
y 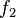 que van del mismo espacio
que van del mismo espacio  al mismo espacio
al mismo espacio 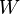 , puedes sumarlas. La nueva función Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (f_1 + f_2)(x) = f_1(x) + f_2(x) también será lineal.
, puedes sumarlas. La nueva función Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (f_1 + f_2)(x) = f_1(x) + f_2(x) también será lineal. - Multiplicación por un número: Si tienes una aplicación lineal
 y un número
y un número  , la función Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (af)(x) = a(f(x)) también es lineal.
, la función Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (af)(x) = a(f(x)) también es lineal. - Composición de aplicaciones lineales: Si tienes una aplicación lineal
 de
de  a
a 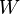 , y otra
, y otra 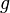 de
de 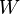 a
a 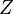 , puedes aplicarlas una después de la otra. La función Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): g \circ f (primero
, puedes aplicarlas una después de la otra. La función Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): g \circ f (primero  , luego
, luego 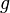 ) también será lineal.
) también será lineal.
Teoremas Clave sobre Transformaciones Lineales
Hay algunos resultados muy importantes sobre las transformaciones lineales:
- Teorema de la base: Si conoces cómo una aplicación lineal transforma las flechas de una base (un conjunto de flechas que "generan" todo el espacio), entonces sabes cómo transforma cualquier otra flecha del espacio. ¡Es única!
- Teorema del rango-nulidad: Para cualquier transformación lineal
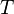 de un espacio
de un espacio  a un espacio
a un espacio 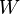 , la dimensión del espacio original
, la dimensión del espacio original  es igual a la suma de la dimensión de su núcleo (nulidad) y la dimensión de su imagen (rango).
es igual a la suma de la dimensión de su núcleo (nulidad) y la dimensión de su imagen (rango).
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \dim(V)=\dim(\operatorname{ker}(T))+\dim (\operatorname{im}(T))
Tipos de Transformaciones Lineales
Las aplicaciones lineales se pueden clasificar según cómo se comportan:
- Monomorfismo: Una aplicación lineal es un monomorfismo si es inyectiva, lo que significa que flechas diferentes en el espacio original siempre se transforman en flechas diferentes en el espacio de llegada. Su núcleo solo contiene la flecha cero.
- Epimorfismo: Una aplicación lineal es un epimorfismo si es sobreyectiva, lo que significa que todas las flechas en el espacio de llegada son el resultado de transformar alguna flecha del espacio original.
- Isomorfismo: Una aplicación lineal es un isomorfismo si es biyectiva (es decir, es inyectiva y sobreyectiva a la vez). Esto significa que hay una correspondencia perfecta entre las flechas de ambos espacios, y la transformación se puede "deshacer" (tiene una inversa lineal).
- Endomorfismo: Es una aplicación lineal donde el espacio de origen y el espacio de llegada son el mismo.
- Automorfismo: Es un endomorfismo que además es biyectivo.
La Matriz Asociada a una Transformación Lineal
Si los espacios vectoriales tienen una dimensión finita (es decir, se pueden describir con un número limitado de flechas base), cualquier aplicación lineal se puede representar con una matriz. Y al revés, cualquier matriz puede representar una aplicación lineal.
Para encontrar la matriz de una transformación lineal 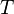 entre dos espacios
entre dos espacios  y
y 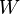 , eliges una base para
, eliges una base para  y otra para
y otra para 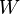 . Luego, aplicas
. Luego, aplicas 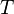 a cada flecha de la base de
a cada flecha de la base de  y escribes el resultado como una combinación de las flechas de la base de
y escribes el resultado como una combinación de las flechas de la base de 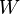 . Los números que usas para esa combinación forman las columnas de la matriz.
. Los números que usas para esa combinación forman las columnas de la matriz.
Esta matriz es única para esas bases elegidas y nos permite hacer cálculos con las transformaciones lineales usando operaciones de matrices.
Galería de imágenes
Véase también
 En inglés: Linear mapping Facts for Kids
En inglés: Linear mapping Facts for Kids

