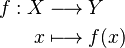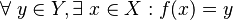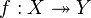Función sobreyectiva para niños
En matemáticas, una función es como una regla que relaciona elementos de un grupo con elementos de otro grupo. Imagina que tienes dos grupos de cosas, por ejemplo, el grupo X y el grupo Y. Una función toma un elemento de X y le asigna un elemento de Y.
Una función se llama sobreyectiva (también conocida como epiyectiva o suprayectiva) cuando cada elemento del segundo grupo (llamado el codominio) es el resultado de aplicar la función a, al menos, un elemento del primer grupo (llamado el dominio).
Piensa en ello así: si la función es como un "lanzador" que envía elementos de X a Y, una función sobreyectiva significa que todos los elementos en Y "reciben" algo. Ningún elemento en Y se queda sin ser "alcanzado".
Formalmente, si tenemos una función:
Esto significa que la función f va del conjunto X al conjunto Y. Para cada elemento x en X, la función f le asigna un elemento f(x) en Y.
Una función es sobreyectiva si para cada elemento y que está en el conjunto Y, siempre puedes encontrar al menos un elemento x en el conjunto X tal que f(x) es igual a y.
Contenido
¿Qué es una función sobreyectiva?
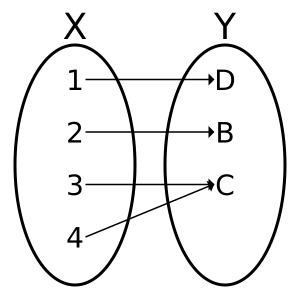
Una función sobreyectiva es una función donde todos los elementos del conjunto de llegada (el codominio) son "alcanzados" por la función. Esto significa que la "imagen" de la función (todos los resultados posibles) es exactamente igual al codominio.
Por ejemplo, si tienes un grupo de estudiantes (conjunto X) y un grupo de casilleros (conjunto Y), y cada estudiante elige un casillero, la función sería sobreyectiva si todos los casilleros son elegidos por al menos un estudiante. No queda ningún casillero vacío.
Simbólicamente, si una función 
va de 
a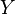 
(
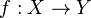), decimos que es sobreyectiva si:
Esto se lee como: "Para todo y que pertenece a Y, existe al menos un x que pertenece a X, tal que el resultado de f(x) es igual a y."
¿Cómo se representa una función sobreyectiva?
A veces, para mostrar que una función 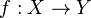es sobreyectiva, se usa una flecha especial con dos puntas:
Esta notación nos indica de forma rápida que la función cubre todo el conjunto de llegada.
Relación entre el tamaño de los conjuntos y la sobreyectividad
Cuando existe una función sobreyectiva de un conjunto 
a un conjunto 
(
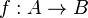), esto nos dice algo importante sobre el tamaño de los conjuntos.
Significa que el número de elementos en el conjunto debe ser mayor o igual que el número de elementos en el conjunto .
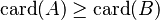
La palabra "card" se refiere a la cantidad de elementos que tiene un conjunto. Es lógico, ¿verdad? Si todos los elementos de son alcanzados por elementos de , entonces no puede ser más pequeño que .
Si además de una función sobreyectiva de a , también existe otra función sobreyectiva de a , entonces se puede demostrar que ambos conjuntos tienen exactamente el mismo número de elementos. Esto se conoce como el teorema de Cantor-Bernstein-Schröder.
Otros tipos de funciones
Véase también
En inglés: Surjective function Facts for Kids
