Antiparalelogramo para niños
Un antiparalelogramo es una figura geométrica de cuatro lados, como un cuadrilátero. Se parece a un paralelogramo porque tiene dos pares de lados opuestos que miden lo mismo. Sin embargo, la diferencia principal es que en un antiparalelogramo, los lados de uno de esos pares se cruzan entre sí. Los lados más largos son siempre los que se cruzan.
A los antiparalelogramos también se les conoce como contraparalelogramos o paralelogramos cruzados. Un paralelogramo cruzado es un tipo especial de cuadrilátero que tiene sus lados cruzados. Una forma particular de paralelogramo cruzado es el rectángulo cruzado, donde los lados más cortos son paralelos.
Contenido
¿Qué hace especial a un Antiparalelogramo?
Simetría y Ángulos
Cada antiparalelogramo tiene una línea de simetría que pasa justo por el punto donde sus lados se cruzan. Gracias a esta simetría, el antiparalelogramo tiene dos pares de ángulos que miden lo mismo, además de sus dos pares de lados iguales.
Junto con las cometas y los trapezoides isósceles, los antiparalelogramos son uno de los tres tipos básicos de cuadriláteros que tienen una línea de simetría.
Vértices en un Círculo
Una característica interesante es que todos los antiparalelogramos son cuadriláteros cíclicos. Esto significa que sus cuatro esquinas (vértices) siempre pueden tocar los bordes de un mismo círculo.
Relación con otras Formas
Si imaginas una línea alrededor de un antiparalelogramo sin que se crucen sus lados, la forma que se crea es un trapezoide isósceles. De hecho, puedes formar un antiparalelogramo usando los lados no paralelos y las diagonales de un trapezoide isósceles.
Antiparalelogramos en Formas 3D
Los antiparalelogramos aparecen en la estructura de muchas figuras tridimensionales complejas, llamadas poliedros no convexos. Por ejemplo, si haces un corte especial cerca de las esquinas de algunos de estos poliedros, la forma que ves en el corte es un antiparalelogramo. Estas formas se llaman "figuras de vértice".
También existen otros poliedros, llamados "poliedros duales", que tienen caras con forma de antiparalelogramos.
Antiparalelogramos en Mecanismos
Conexiones de Cuatro Barras
El antiparalelogramo se ha usado mucho en el diseño de mecanismos de cuatro barras. Imagina cuatro barras rígidas (los lados del antiparalelogramo) unidas por articulaciones en sus esquinas. Estas barras pueden girar unas respecto a otras. A este tipo de mecanismo también se le llama "mariposa" o "conexión de lazo de pajarita".
Si fijas uno de los lados cortos (los que no se cruzan) de un antiparalelogramo, y dejas que las otras barras se muevan libremente, el punto donde los lados se cruzan dibujará una elipse. Los extremos del lado fijo serán los puntos clave de esa elipse.
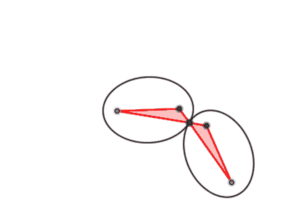
Movimiento de Puntos
Si fijas uno de los lados largos (los que se cruzan) de un antiparalelogramo, las articulaciones libres se moverán en círculos. A diferencia de un paralelogramo, donde los puntos se mueven en la misma dirección, en un antiparalelogramo se mueven en direcciones opuestas.
El inventor James Watt descubrió que si un antiparalelogramo tiene su lado largo fijo, el punto medio del lado largo que se mueve describe una curva con forma de ocho, llamada lemniscata.
Aplicaciones en Ingeniería
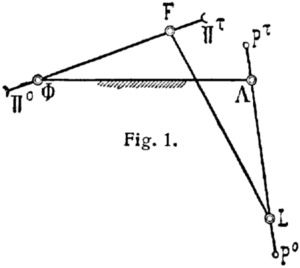
El antiparalelogramo es una parte importante del mecanismo inversor de Hart. Este mecanismo, al igual que el mecanismo de Peaucellier–Lipkin, puede transformar un movimiento de giro en un movimiento en línea recta.
También se usan pares de antiparalelogramos para conectar los ejes de los vehículos de cuatro ruedas. Esto ayuda a controlar cómo se tuerce la suspensión del vehículo, permitiendo que solo un eje gire.
El matemático Alfred Kempe usó pares de antiparalelogramos en un sistema que llamó "multiplicador". Con este sistema, se podía dibujar cualquier curva algebraica o multiplicar un ángulo por un número entero.
Antiparalelogramos en el Espacio
En el estudio de cómo se mueven varios cuerpos celestes bajo la fuerza de la gravedad, se ha encontrado que existen configuraciones donde los cuerpos giran alrededor de un punto central como si estuvieran unidos. Para cuatro cuerpos con masas iguales, se ha visto que hay una serie de configuraciones que están relacionadas con el movimiento de un antiparalelogramo articulado.
Véase también
 En inglés: Polygon Facts for Kids
En inglés: Polygon Facts for Kids