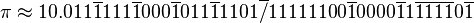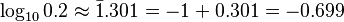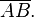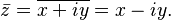Vinculum (símbolo) para niños
Un vinculum es una línea horizontal que se usa en las matemáticas para un propósito especial. Puede ir encima (sobrerayado) o debajo (subrayado) de una expresión matemática. Su función es indicar que todos los números o símbolos bajo esa línea deben considerarse como un solo grupo.
El vinculum también es la línea que separa la parte de arriba (numerador) de la parte de abajo (denominador) en una fracción.
Antiguamente, el vinculum se usaba mucho para agrupar elementos en matemáticas escritas. Sin embargo, hoy en día, esta función se ha reemplazado casi por completo con el uso de los paréntesis. Aun así, el vinculum todavía se usa comúnmente para señalar los números que se repiten en un decimal periódico. Este uso es una excepción importante y muestra cómo se usaba originalmente.
La palabra Vinculum viene del latín y significa ‘vínculo’, ‘traba’, ‘cadena’ o ‘lazo’. Esto nos da una idea de cómo se usa este símbolo.
Contenido
¿Para qué se usa el vinculum en matemáticas?
El vinculum tiene varios usos importantes en matemáticas.
Indicar un segmento de línea
Un vinculum puede mostrar un segmento de línea. Por ejemplo, si tienes los puntos A y B, la línea sobre ellos 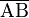 indica el segmento que los une.
indica el segmento que los une.
Mostrar decimales que se repiten
El vinculum se usa para indicar que un valor decimal periódico se repite sin fin. Por ejemplo:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{1}{7} = 0,\overline{142857}
Esto significa que los números 142857 se repiten una y otra vez: 0,142857142857142857...
También se usa para mostrar los términos que se repiten en una fracción continua. Los números irracionales cuadráticos son los únicos números que tienen un vinculum en su representación de fracción continua.
Agrupar operaciones matemáticas
Su uso principal en el pasado era para agrupar operaciones. Funcionaba como los paréntesis de hoy. Por ejemplo:
Esto significaba que primero debías sumar b y c, y luego restar ese resultado de a. Hoy en día, esto se escribiría más comúnmente como a − (b + c). Los paréntesis, tal como los conocemos para agrupar, no se encontraban mucho en los libros de matemáticas antes del siglo XVIII. El vinculum se usaba mucho, generalmente como una línea superior. Sin embargo, Nicolas Chuquet en 1484 usó la versión de línea inferior.
En la notación de raíces (radicales)
El vinculum es parte de la notación de un radical (como la raíz cuadrada). Indica la cantidad a la que se le está calculando la raíz. Por ejemplo, en la siguiente expresión, la cantidad  es el radicando, por eso tiene un vinculum encima:
es el radicando, por eso tiene un vinculum encima:
En 1637, René Descartes fue el primero en combinar el símbolo de raíz alemán (√) con el vinculum para crear el símbolo de radical que usamos hoy.
A veces, el vinculum no tiene que ser una línea recta. En algunos casos, se pueden usar paréntesis o corchetes para señalar la agrupación.
¿Qué otras notaciones se parecen al vinculum?
Existen varias notaciones matemáticas que usan una línea superior y que pueden confundirse fácilmente con un vinculum.
Dígitos negativos
Puede usarse en el sistema de dígitos signados para representar números negativos. Por ejemplo, en el sistema ternario equilibrado:
Logaritmos
También se usa en la notación de "barra" en logaritmos comunes, como:
Álgebra Booleana
En el Álgebra de Boole, la línea superior a veces se usa para indicar que un grupo de expresiones debe ser negado (su resultado lógico se invierte), como en:
En electrónica, esta línea horizontal superior se usa a menudo para señalar señales binarias complementarias. Por ejemplo, "READY" (listo) con una línea encima significa "no listo", que es la misma señal pero con la polaridad opuesta. Este uso está muy relacionado con el álgebra Booleana.
Números complejos
También se usa para referirse al conjugado de un número complejo:
Estadísticas
En estadísticas, la línea horizontal superior puede usarse para indicar el promedio de una serie de valores.
Física de partículas
En la física de partículas, la línea horizontal superior suele indicar antipartículas. Por ejemplo, p y p son los símbolos para protón y antiprotón, respectivamente.
Vectores
El vinculum no debe confundirse con la notación de un vector, que se ve similar. Por ejemplo: 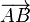 significa "Vector de A a B", o
significa "Vector de A a B", o 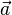 significa "vector "a"". Aunque a veces se usa una línea superior o inferior sin la punta de la flecha en su lugar (por ejemplo:
significa "vector "a"". Aunque a veces se usa una línea superior o inferior sin la punta de la flecha en su lugar (por ejemplo: 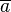 o
o 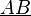 ).
).
¿Se usaba en los números romanos?
Se ha dicho que en la numeración romana, un vinculum podía indicar que los números debajo de la línea representaban mil veces su valor original. El historiador de las matemáticas David Eugene Smith no estaba de acuerdo con esto. Sin embargo, esta notación sí se usó en la Edad Media.
Véase también
 En inglés: Vinculum (symbol) Facts for Kids
En inglés: Vinculum (symbol) Facts for Kids


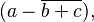
![\sqrt[n]{ab+2}\,.](/images/math/9/6/b/96ba89a1e9eac34563e5652eb301eee9.png)