Triángulo de Reuleaux para niños
Plantilla:Ficha de entidad geométrica El triángulo de Reuleaux es una forma geométrica muy interesante. Imagina un triángulo con lados curvos en lugar de rectos. Lo más especial de este triángulo es que tiene una "anchura constante". Esto significa que si lo mides de un lado a otro, la distancia siempre será la misma, no importa cómo lo gires. Es como un círculo, que también tiene anchura constante, pero el triángulo de Reuleaux es la forma más sencilla con esta propiedad que no es un círculo.
Esta forma recibe su nombre de Franz Reuleaux, un ingeniero alemán del siglo XIX. Él estudió mucho cómo funcionan las máquinas y cómo se mueven las cosas, y usó este tipo de triángulos en sus diseños.
Aunque lleva su nombre, el triángulo de Reuleaux ya era conocido antes de su época. Por ejemplo, se puede ver en el diseño de algunas ventanas de iglesias antiguas. También Leonardo da Vinci lo usó para un tipo de mapa, y el matemático Leonhard Euler lo estudió.
Contenido
¿Qué hace especial al Triángulo de Reuleaux?
El triángulo de Reuleaux es especial por varias razones:
- Es la forma de anchura constante más simple después del círculo.
- Tiene el área más pequeña posible entre todas las formas con la misma anchura constante.
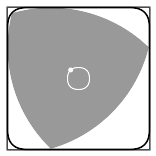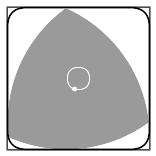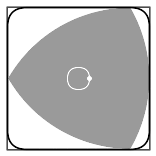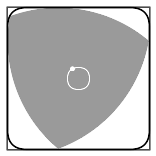
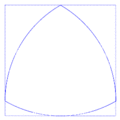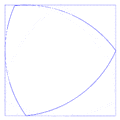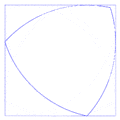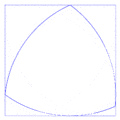
- Puede girar completamente dentro de un cuadrado, tocando siempre los cuatro lados. Por esta razón, a veces se le llama "rotor de Reuleaux".
¿Cómo se forma un Triángulo de Reuleaux?
Para crear un triángulo de Reuleaux, necesitas tres círculos.
- Imagina un triángulo equilátero (todos sus lados y ángulos son iguales).
- Ahora, desde cada esquina de ese triángulo, dibuja un arco de círculo. El centro de cada arco es una esquina del triángulo, y el radio del arco es la longitud del lado del triángulo.
- Cuando dibujes los tres arcos, la forma que queda en el centro es el triángulo de Reuleaux.
Cada ángulo de un triángulo equilátero mide 60 grados. El perímetro de un triángulo de Reuleaux de anchura a es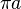 
.
Usos del Triángulo de Reuleaux
Aunque parezca una forma curiosa, el triángulo de Reuleaux tiene varias aplicaciones prácticas:
Tapas de alcantarilla
Una pregunta común es: "Además de un círculo, ¿qué otra forma puede tener una tapa de alcantarilla para que no se caiga por el agujero?". La respuesta es cualquier forma de anchura constante, y el triángulo de Reuleaux es un ejemplo perfecto. Como su anchura es siempre la misma, no importa cómo la gires, nunca se caerá por un agujero cuadrado del mismo tamaño.
Herramientas y objetos cotidianos
- Algunas púas de guitarra tienen esta forma.
- Ciertos lápices se fabrican con este perfil. Son más cómodos de sujetar y es menos probable que rueden de las mesas.
- Existen brocas especiales, como la broca de Harry Watts, que tienen forma de triángulo de Reuleaux. Estas brocas, con un mecanismo especial, pueden taladrar agujeros que son casi perfectamente cuadrados.
Mecanismos y máquinas
- El rotor de un Motor Wankel (un tipo de motor de combustión) se parece mucho a un triángulo de Reuleaux, aunque sus lados son un poco más planos.
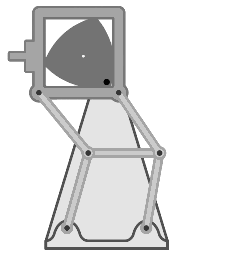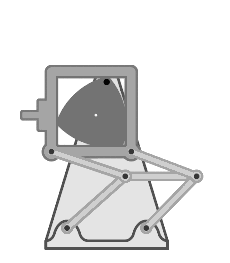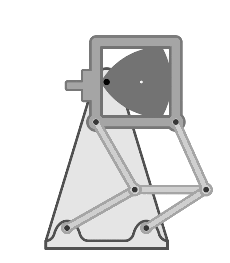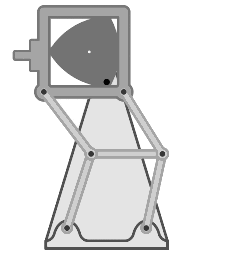
- En los proyectores de cine, se usa un mecanismo basado en el triángulo de Reuleaux. Este mecanismo ayuda a que la película avance de forma escalonada: se detiene un momento para mostrar cada imagen y luego se mueve rápidamente a la siguiente.
Monedas
El concepto de anchura constante es muy útil para las monedas. Permite que las máquinas que funcionan con monedas las acepten sin importar cómo entren. Algunas monedas, como las de 20 peniques del Reino Unido, usan una forma similar al triángulo de Reuleaux, pero con más lados (un heptágono de Reuleaux). También se ha usado un triángulo de Reuleaux para una moneda conmemorativa en Bermudas.
Generalizaciones del Triángulo de Reuleaux
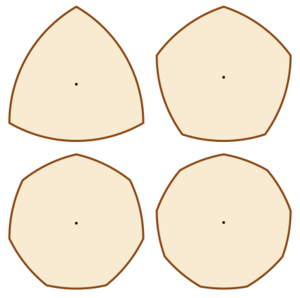
El triángulo de Reuleaux es solo el primero de una familia de formas llamadas "polígonos de Reuleaux". Estos se crean a partir de polígonos regulares con un número impar de lados, y todos tienen la propiedad de anchura constante.
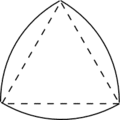
También existen versiones tridimensionales. Por ejemplo, el tetraedro de Reuleaux se forma a partir de la intersección de cuatro esferas. Aunque no tiene anchura constante por sí mismo, se puede modificar para crear el tetraedro de Meissner, que sí la tiene.
Galería de imágenes
-
El triángulo de Reuleaux, en cualquier orientación, siempre es tangente a un cuadrado
-
El triángulo de Reuleaux es una curva de anchura constante basada en un triángulo equilátero. La distancia entre cualquier punto de una de las curvas y el vértice opuesto es la misma.
-
Rodillos con sección circular y de triángulo de Reuleaux. Deutsche Technikmuseum, Berlín
-
Cuatro bolas se intersecan para formar un tetraedro de Reuleaux.
-
Triquetra entrelazados para formar un nudo trébol
Véase también
En inglés: Reuleaux triangle Facts for Kids
