Sistema de todos contra todos para niños
El sistema de todos contra todos o sistema de liga es una forma de organizar torneos deportivos. En este sistema, cada participante o equipo se enfrenta a todos los demás al menos una vez. Es como una "liguilla" donde todos juegan contra todos. A diferencia de los torneos de eliminación, donde el que pierde queda fuera, aquí todos siguen jugando hasta que se han enfrentado a cada rival.
Este tipo de competición es muy común en las ligas nacionales de deportes como el baloncesto, el béisbol, el fútbol y el rugby. En estas ligas, los equipos juegan durante varias semanas o meses.
En algunas copas internacionales importantes, como la Copa Mundial de Fútbol o la Liga de Campeones de la UEFA, se usa una combinación de sistemas. Primero, los equipos se dividen en grupos pequeños (por ejemplo, de cuatro) y juegan todos contra todos. Los mejores de cada grupo avanzan a una segunda fase, que ya es de eliminación directa.
Contenido
¿Cuáles son las Desventajas de este Sistema?
Una desventaja de este sistema, especialmente cuando hay pocos equipos, es el "círculo de la muerte". Esto ocurre cuando varios equipos terminan con la misma puntuación, pero se han ganado entre sí en un círculo. Por ejemplo, si el equipo A le gana al B, el B le gana al C, y el C le gana al A, todos tendrían una victoria y una derrota. En estos casos, se necesitan reglas adicionales para decidir quién clasifica.
¿Cómo se Clasifican los Equipos?
Para saber quién va ganando en un torneo de liga, se usan tablas de clasificación. A cada equipo se le dan puntos según los resultados de sus partidos. En el fútbol, por ejemplo:
- Una victoria da 3 puntos.
- Un empate da 1 punto.
- Una derrota da 0 puntos.
Este sistema de puntuación se hizo popular en los años 80 y 90, reemplazando uno antiguo donde la victoria valía 2 puntos.
A veces, la puntuación no es suficiente para decidir todas las posiciones, sobre todo si hay empates. Por eso, se usan otros criterios para desempatar, que pueden variar en cada torneo. Lo más común es fijarse en la cantidad de goles marcados y recibidos.
La Copa Mundial de Fútbol usa los siguientes criterios para desempatar si dos o más equipos tienen los mismos puntos:
- Mayor diferencia de goles (goles a favor menos goles en contra).
- Mayor número de goles anotados.
- Mayor número de puntos obtenidos en los partidos entre los equipos empatados.
- Mayor diferencia de goles en los partidos entre los equipos empatados.
- Mayor número de goles anotados en los partidos entre los equipos empatados.
- Un sorteo realizado por los organizadores.
Un ejemplo de cómo funciona la clasificación es el Grupo B de la Copa Mundial de Fútbol de 1998: Italia quedó primera porque ganó dos partidos y empató uno. Chile quedó segunda con tres empates. Austria quedó tercera, aunque tenía los mismos puntos que Camerún, porque tuvo una mejor diferencia de goles (–1 contra –3).
|
|
¿Cómo se Organizan los Partidos?
Para organizar los partidos de un torneo de todos contra todos, se usa un calendario llamado fixture. Este calendario asegura que cada equipo juegue contra todos los demás.
Si hay n equipos, en una ronda simple se necesitan un total de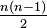 
partidos. Por ejemplo, si hay 4 equipos, se necesitan Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \begin{matrix} \frac{4(4-1)}{2} \end{matrix} = 6 partidos.
Para crear el calendario, se puede asignar un número a cada equipo y luego rotar los números, dejando uno fijo. Por ejemplo, en un torneo con 14 equipos:
- 1.ª ronda: 1 contra 14, 2 contra 13, y así sucesivamente.
- 2.ª ronda: 1 contra 13, 14 contra 12, y así.
Este proceso se repite hasta que todos hayan jugado contra todos.
El Sistema de Todos contra Todos en el Tenis
En el tenis, este sistema se conoce como round robin. Se usa en algunos torneos importantes como las ATP World Tour Finals y las WTA Finals. En estos torneos, los jugadores se dividen en grupos de tres o cuatro. Cada jugador juega al menos dos partidos dentro de su grupo. Los mejores de cada grupo avanzan a una fase de eliminación directa, donde el que pierde queda fuera.
Este formato busca que el público pueda ver a sus jugadores favoritos más veces en un mismo torneo. La ATP lo probó en 2007, pero generó confusión en algunos jugadores y se dejó de usar en la mayoría de los torneos.
Existen diferentes formas de organizar los grupos según el número de participantes:
- 24 jugadores: Se forman ocho grupos de tres tenistas. Los ganadores de cada grupo pasan a los cuartos de final, donde empieza la eliminación directa.
- 32 jugadores: Primero hay una fase de "play-offs" con 16 jugadores. Los 8 ganadores se unen a otros 16 jugadores. Luego, se forman ocho grupos de tres tenistas. Los ganadores de cada grupo avanzan a los cuartos de final.
- 48 jugadores: Se forman dieciséis grupos de tres jugadores. Los ganadores de cada grupo avanzan a los octavos de final.
Véase también
En inglés: Round-robin tournament Facts for Kids
