Topología geométrica para niños
La topología geométrica es una rama de las matemáticas que estudia las formas y los espacios, especialmente aquellos que tienen pocas dimensiones, como una línea (1D), una superficie (2D), un objeto sólido (3D) o incluso el espacio-tiempo (4D). Imagina que tienes una figura hecha de plastilina. La topología geométrica se interesa en cómo puedes estirar, doblar o retorcer esa figura sin romperla ni pegarla.
Esta área de la topología y la topología algebraica busca resolver problemas relacionados con la forma y la estructura de los objetos. Se inspira en cómo se comportan las cosas en el mundo real, como los fenómenos físicos, y también en ideas abstractas sobre las dimensiones. Se enfoca mucho en las formas en tres y cuatro dimensiones.
Algunos de los temas más importantes que estudia la topología geométrica son:
- La teoría de nudos, que analiza cómo se pueden anudar las cuerdas en el espacio.
- La clasificación de las formas en 3 y 4 dimensiones.
- La famosa Conjetura de Poincaré, un problema matemático muy importante que fue resuelto hace poco.
La topología geométrica es una ciencia que conecta muchas ramas de las matemáticas entre sí y también con otras áreas como la física.
Contenido
Explorando Formas y Espacios: Tópicos Clave
La topología geométrica nos ayuda a entender diferentes tipos de formas y cómo se relacionan.
Formas de una Dimensión (1-variedades)
Las formas de una dimensión son como líneas o caminos.
- Curva: Es un camino que puedes dibujar entre dos puntos en el espacio.
- Trayectoria: Similar a una curva, pero no tiene que ser "suave" en todos sus puntos, solo continua.
- Circunferencia o 1-esfera: Es cualquier camino cerrado y simple, como un círculo.
- Nudo: En matemáticas, un nudo es como una cuerda anudada que no tiene extremos sueltos, es decir, forma un círculo cerrado en el espacio.
- Enlace: Es un conjunto de varios nudos que están entrelazados entre sí.
- Trenza: Es un conjunto de hilos que se entrelazan, como una trenza de pelo, pero con los extremos fijos.
- Nudo tórico: Es un tipo especial de nudo que se puede dibujar sobre la superficie de un toro (una forma de dona).
Formas de Dos Dimensiones (2-variedades)
Las formas de dos dimensiones son como superficies.
- Superficie: Es la "piel" o el exterior de objetos tridimensionales. Son formas que, si las miras de cerca, parecen un plano.
- Esfera: La superficie de una pelota.
- Toro: La superficie de una dona.
- Botella de Klein: Es una superficie muy curiosa que no tiene "adentro" ni "afuera" y no tiene borde. Es como una banda de Möbius pero en 3D.
- Banda de Möbius: Es una superficie con un solo lado y un solo borde. Puedes hacer una doblando una tira de papel y pegando sus extremos después de darle media vuelta.
- Característica de Euler: Es un número que ayuda a describir una superficie. Se calcula restando el número de lados al número de vértices y sumando el número de caras de una figura. Este número no cambia aunque deformes la superficie.
Formas de Tres Dimensiones (3-variedades)
Las formas de tres dimensiones son como los objetos sólidos que nos rodean.
- 3-esfera: Es la superficie de una esfera en cuatro dimensiones. Es difícil de imaginar, pero es un concepto importante en matemáticas.
- Poliedros: Son objetos tridimensionales con caras planas, como un cubo o una pirámide.
- Conjetura de Poincaré: Es una de las preguntas más famosas de la topología. Dice que si un espacio tridimensional cerrado y sin agujeros es "simplemente conexo" (es decir, cualquier lazo en él se puede encoger a un punto), entonces debe ser como una esfera tridimensional. Fue demostrada por el matemático Grigori Perelman en 2006.
- Espacio hiperbólico: Es un tipo de espacio donde las líneas paralelas se separan más rápidamente que en el espacio normal.
Formas de Cuatro Dimensiones (4-variedades)
Las formas de cuatro dimensiones son más abstractas, pero son importantes en la física.
- Espacio-tiempo: En la Relatividad, el espacio-tiempo combina las tres dimensiones del espacio con la dimensión del tiempo.
Conceptos Generales de Variedades
Las "variedades" son los objetos principales que estudia la topología geométrica. Son espacios que, si los miras de cerca, se parecen a un espacio euclídeo (como una línea, un plano o un espacio 3D).
- Homeomorfismo: Es como una "equivalencia" entre dos formas. Dos formas son homeomorfas si puedes transformar una en la otra estirándola, doblándola o retorciéndola, sin romperla ni pegarla. Por ejemplo, una taza de café y una dona son homeomorfas porque puedes deformar una en la otra.
- Suma conexa: Es una forma de "pegar" dos variedades quitando un pequeño disco de cada una y uniendo los bordes resultantes.
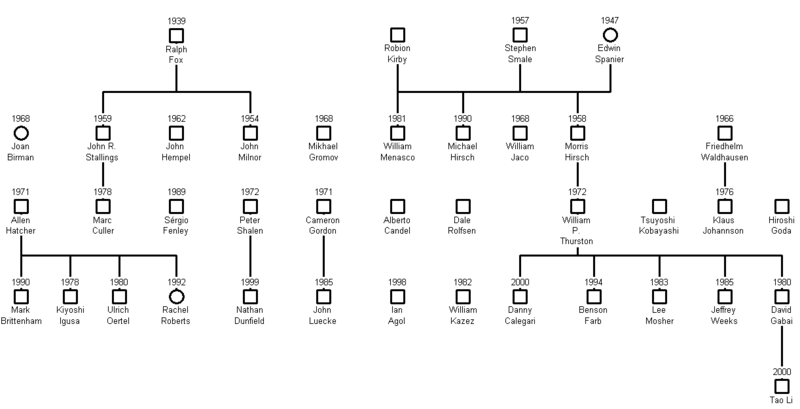
Personas Importantes en Topología Geométrica
Muchos matemáticos brillantes han contribuido al desarrollo de la topología geométrica, explorando las propiedades de las formas y los espacios.
Ver También
- Topología algebraica: Otra rama de la topología que usa herramientas del álgebra para estudiar los espacios.
- Topología diferencial: Estudia las propiedades de los espacios que tienen una estructura "suave" o diferenciable.
- Teoría geométrica de grupos: Combina la teoría de grupos con la geometría.
Véase también
 En inglés: Geometric topology Facts for Kids
En inglés: Geometric topology Facts for Kids