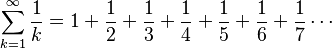Serie armónica (matemática) para niños
La serie armónica en matemáticas es una suma especial de números. Se forma sumando los inversos de los números enteros positivos, uno por uno.
Se ve así:
|
|
Se le llama "armónica" por su relación con la música. Cuando una cuerda vibra, produce sonidos llamados armónicos. La longitud de onda de estos armónicos es proporcional a la longitud de onda del sonido principal. Los factores de esa proporción son justo los términos de esta serie: 1, 1/2, 1/3, 1/4, y así sucesivamente. El primer término (1) representa el sonido fundamental.
Contenido
¿Qué es la Serie Armónica?
La serie armónica es una serie infinita, lo que significa que tiene un número ilimitado de términos que se van sumando. Cada término es una fracción donde el numerador es 1 y el denominador es un número entero positivo que va aumentando (1, 2, 3, 4, etc.).
¿Por qué se llama "armónica"?
El nombre "armónica" viene de la física y la música. Imagina una cuerda de guitarra que vibra. Además de su sonido principal, produce otros sonidos más suaves llamados armónicos. Estos armónicos tienen frecuencias que son múltiplos de la frecuencia fundamental. Las longitudes de onda de estos armónicos se relacionan con la longitud de onda fundamental mediante fracciones como 1/2, 1/3, 1/4, etc. Estas fracciones son exactamente los términos de la serie armónica.
¿La Serie Armónica Crece Sin Parar?
Una de las propiedades más interesantes de la serie armónica es que es "divergente". Esto significa que, aunque los términos que se suman son cada vez más pequeños, la suma total nunca llega a un número fijo. ¡Sigue creciendo y creciendo sin límite!
¿Cómo sabemos que la serie armónica diverge?
Aunque parezca que la suma debería detenerse porque los números son cada vez más pequeños, no es así. Un matemático llamado Nicolás Oresme demostró esto alrededor del año 1350. Su idea fue agrupar los términos de la serie de una manera especial:
- 1
- 1/2
- (1/3 + 1/4)
- (1/5 + 1/6 + 1/7 + 1/8)
- Y así sucesivamente.
Si miras los grupos, verás que:
- (1/3 + 1/4) es mayor que (1/4 + 1/4), que es igual a 1/2.
- (1/5 + 1/6 + 1/7 + 1/8) es mayor que (1/8 + 1/8 + 1/8 + 1/8), que también es igual a 1/2.
Así, puedes ver que la suma de la serie armónica es mayor que la suma de 1 + 1/2 + 1/2 + 1/2 + ... Esta última suma claramente crece sin límite, por lo tanto, la serie armónica también lo hace.
La Serie Armónica Alternada: Un Caso Diferente
Existe una versión de la serie armónica llamada serie armónica alternada. En esta serie, los signos de los términos se van cambiando: uno es positivo, el siguiente negativo, luego positivo, y así sucesivamente.
Se ve así: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sum_{k = 1}^\infty \frac{(-1)^{k + 1}}{k} = 1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \frac{1}{5} - \frac{1}{6} + \frac{1}{7} \cdots
A diferencia de la serie armónica original, la serie armónica alternada sí "converge". Esto significa que su suma se acerca a un valor específico a medida que se añaden más términos. Ese valor es el logaritmo natural de 2, que es aproximadamente 0.693.
Serie Armónica Parcial
Cuando sumamos solo los primeros n términos de la serie armónica, obtenemos lo que se llama el n-ésimo número armónico, que se representa como Hn.
Se define así: 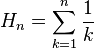
Por ejemplo:
- H1 = 1
- H2 = 1 + 1/2 = 1.5
- H3 = 1 + 1/2 + 1/3 = 1.833...
El valor de Hn crece de forma similar al logaritmo natural de n. A medida que n se hace muy grande, la diferencia entre Hn y el logaritmo natural de n se acerca a un número especial llamado la constante de Euler-Mascheroni, que se representa con la letra griega gamma (γ).
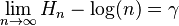
Un dato curioso es que el único Hn que es un número entero es H1 (que es 1).
Las p-series
Las p-series son un tipo de series matemáticas que se parecen a la serie armónica, pero con una pequeña diferencia. En lugar de tener solo n en el denominador, tienen n elevado a una potencia p.
Se ven así: 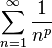
Aquí, p es un número real positivo.
- Si p es mayor que 1 (por ejemplo, 2, 3, 1.5), la p-serie es "convergente", lo que significa que su suma se acerca a un valor fijo.
- Si p es igual o menor que 1 (por ejemplo, 1, 0.5), la p-serie es "divergente", lo que significa que su suma crece sin límite.
La serie armónica original es un caso especial de la p-serie, donde p es igual a 1. Por eso, la serie armónica es divergente.
Véase también
 En inglés: Harmonic series (mathematics) Facts for Kids
En inglés: Harmonic series (mathematics) Facts for Kids
- Media armónica
- Número armónico