Rotación impropia para niños

En geometría, una rotación impropia, también conocida como rotorreflexión o reflexión rotativa, es un tipo especial de movimiento que combina dos acciones: una rotación alrededor de un eje y una reflexión (como en un espejo) en un plano que es perpendicular a ese eje. Imagina que giras un objeto y luego lo reflejas.

¿Qué es la rotorreflexión en tres dimensiones?

Subgrupos de los grupos de Schoenflies S₂ hasta S₂₀

En el espacio tridimensional, la rotorreflexión también se puede entender como la combinación de una rotación y una simetría central (invertir el objeto a través de un punto). Por eso, a veces se le llama rotoinversión. Si un objeto tiene un solo punto que no se mueve durante esta transformación, entonces esa transformación es una rotación impropia.

Es interesante saber que, en ambos casos (rotación + reflexión o rotación + inversión), las operaciones se pueden hacer en cualquier orden y el resultado será el mismo. Una rotorreflexión y una rotoinversión son muy parecidas; la diferencia principal es el ángulo de rotación.

Cuando un objeto sufre una rotación impropia, lo que realmente se rota es su imagen reflejada. El eje alrededor del cual ocurre la rotación se llama eje de rotación-reflexión. Si el ángulo de rotación es de 360° dividido por un número n, se le llama una n-variedad de rotación impropia.

Existen diferentes formas de nombrar estas rotaciones impropias:

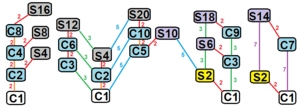
• La notación de Schoenflies usa el símbolo S_n para un grupo de simetría. Por ejemplo, S₆ significa una rotación de 60° (360°/6) combinada con una reflexión.
• La notación de Hermann–Mauguin usa el símbolo n para una n-variedad de rotoinversión, que es una rotación de 360°/n con una inversión.

Ejemplos de objetos con simetría de rotorreflexión

Muchos objetos y formas geométricas tienen simetría de rotorreflexión. Un buen ejemplo son los antiprismas. Un antiprisma es una figura geométrica con dos bases paralelas que son polígonos, y sus lados son triángulos.

Ejemplos de poliedros con simetría de rotorreflexión

Grupo	S4	S6	S8	S10	S12
Ejemplo	Antiprisma digonal biselado	Octaedro	Antiprisma cuadrado	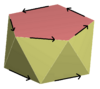Antiprisma pentagonal	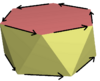Antiprisma hexagonal

Los antiprismas tienen esta simetría especial a lo largo de ciertas aristas. Si un antiprisma tiene un número impar de lados en sus bases (como un antiprisma pentagonal), también puede tener simetría central.

¿Qué es una isometría indirecta?

En un sentido más amplio, una rotación impropia es un tipo de isometría indirecta. Una isometría es un movimiento que mantiene las distancias y las formas de los objetos. Las isometrías indirectas son aquellas que cambian la "orientación" del objeto, como si lo vieras en un espejo. Esto incluye las reflexiones puras o las reflexiones con un deslizamiento.

Por otro lado, una rotación propia es una rotación normal. Se considera una isometría directa, lo que significa que no cambia la orientación del objeto. Esto incluye la identidad (no mover nada), una rotación con un movimiento en el eje, o solo un movimiento puro.

Es importante saber que si combinas dos rotaciones impropias, el resultado siempre será una rotación propia. Y si combinas una rotación impropia con una rotación propia, el resultado será una rotación impropia.

¿Por qué es importante en la ciencia?

Cuando los científicos estudian la simetría de un sistema físico (por ejemplo, cómo se organizan los átomos en un cristal), es muy importante entender las rotaciones impropias. Esto ayuda a distinguir entre diferentes tipos de cantidades físicas, como los vectores (que tienen dirección y magnitud) y los pseudovectores (que se comportan de manera diferente bajo estas transformaciones de simetría).

Véase también

En inglés: Improper rotation Facts for Kids

• Isometría
• Grupo ortogonal