Punto de inflexión para niños
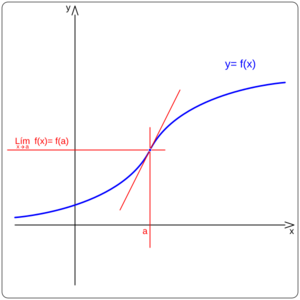
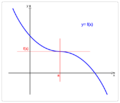
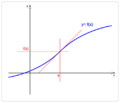
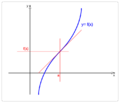
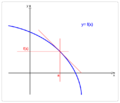
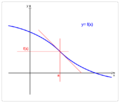
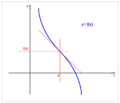
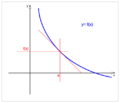
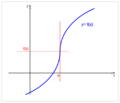
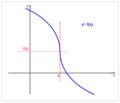
En matemáticas, un punto de inflexión de una función es un lugar especial en su gráfica. Imagina que estás dibujando una línea curva. Un punto de inflexión es el sitio exacto donde la curva cambia la forma en que se dobla. Pasa de curvarse hacia arriba a curvarse hacia abajo, o viceversa. Es como si la curva cambiara de dirección en su "curvatura".
En estos puntos, la línea que toca la curva en ese lugar (llamada tangente) parece "atravesar" la curva.
Contenido
¿Qué es un Punto de Inflexión en Matemáticas?
Un punto de inflexión es un concepto importante cuando estudiamos cómo se comportan las funciones en sus gráficas. Nos ayuda a entender la forma de la curva.
Entendiendo la concavidad
Para entender un punto de inflexión, primero necesitamos saber qué es la concavidad.
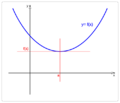
- Una curva es cóncava hacia arriba (o convexa) si se parece a una "U" o a una sonrisa. Piensa en una taza que puede contener agua.
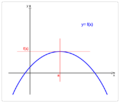
- Una curva es cóncava hacia abajo (o cóncava) si se parece a una "U" invertida o a un ceño fruncido. Piensa en una taza volteada.
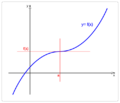
Un punto de inflexión es el lugar donde la curva cambia de ser cóncava hacia arriba a cóncava hacia abajo, o al revés.
¿Cómo se encuentra un Punto de Inflexión?
Para encontrar estos puntos en una función, los matemáticos usan una herramienta llamada la "segunda derivada". Si la segunda derivada de una función es cero en un punto, o no existe, ese punto podría ser un punto de inflexión.
Aquí te explicamos los pasos generales, de forma sencilla:
- Primero, se calcula la "segunda derivada" de la función. Esto es como medir cómo cambia la pendiente de la curva.
- Luego, se busca dónde esta segunda derivada es igual a cero. Esos son los posibles puntos de inflexión.
- Finalmente, se verifica si la curva realmente cambia su forma de doblarse en esos puntos. Si lo hace, ¡felicidades, encontraste un punto de inflexión!
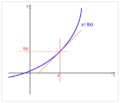
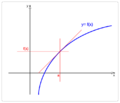
Por ejemplo, una función como 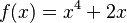 no tiene puntos de inflexión. Esto se debe a que su segunda derivada siempre es mayor o igual a cero, lo que significa que la curva siempre se dobla de la misma manera, sin cambiar su concavidad.
no tiene puntos de inflexión. Esto se debe a que su segunda derivada siempre es mayor o igual a cero, lo que significa que la curva siempre se dobla de la misma manera, sin cambiar su concavidad.
Galería de imágenes
Véase también
 En inglés: Inflection point Facts for Kids
En inglés: Inflection point Facts for Kids
- Punto crítico
- Punto fronterizo
- Punto estacionario
- Punto singular
- Punto de inflexión
- Extremos de una función
- Singularidad matemática
- Clasificación de discontinuidades
- Criterio de la primera derivada
- Criterio de la segunda derivada
- Criterio de la tercera derivada
- Criterio de la derivada de mayor orden
- Punto de silla