Singularidad matemática para niños
En el mundo de las funciones matemáticas, a veces nos encontramos con situaciones un poco misteriosas. Una singularidad de la función ocurre cuando una función matemática se comporta de una manera muy inusual o inesperada en un punto específico. Es como si las reglas normales de la función dejaran de funcionar en ese lugar.
Contenido
¿Qué es una Singularidad en Matemáticas?
Imagina que estás siguiendo un camino en un mapa (que es como una función). De repente, llegas a un punto donde el camino simplemente desaparece o se convierte en un agujero sin fondo. Eso es lo que pasa con una singularidad en matemáticas. Es un punto donde la función no tiene un valor claro o se vuelve infinitamente grande o pequeña.
Un Ejemplo Sencillo: Dividir por Cero
Uno de los ejemplos más fáciles de entender es la división por cero. Sabemos que no podemos dividir un número entre cero. Por ejemplo, si intentas calcular 40 dividido por 0, no hay un número que, multiplicado por 0, te dé 40. ¡Simplemente no existe! En matemáticas, decimos que la división por cero es una operación "indefinida" o que produce una singularidad.
¿Cómo se Relaciona con la Continuidad?
Para entender mejor las singularidades, pensemos en la idea de "continuidad". Una función es continua si puedes dibujarla en un papel sin levantar el lápiz. Es como un camino suave y sin interrupciones.
Tipos de Interrupciones en las Funciones
Cuando una función no es continua, decimos que tiene una "discontinuidad". Las singularidades son un tipo especial de discontinuidad.
- Discontinuidades de salto: Imagina que el camino se interrumpe y tienes que saltar para seguir.
* De salto puntual: El camino tiene un pequeño agujero, pero luego sigue igual. * De salto finito: El camino salta a un nivel diferente y continúa. * De salto infinito: Aquí es donde el camino se va hacia arriba o hacia abajo sin fin, ¡hacia el infinito! Estas son las que llamamos singularidades.
Ejemplos de Funciones con Singularidades
Muchas funciones matemáticas comunes tienen singularidades. Aquí te mostramos algunas:
- La función Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): y(x)=\frac{1}{x} : Esta función es una hipérbola. Si intentas poner
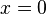en esta función, obtendrás Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{1}{0} , que no tiene un valor definido. En este punto, la función se dispara hacia el infinito (o menos infinito), creando una singularidad. Es como si la gráfica de la función se acercara mucho a una línea (llamada asíntota) pero nunca la tocara.
- Funciones racionales: Cualquier función que sea una fracción (como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): y(x)=\frac{2x-8}{4x-12} ) tendrá una singularidad si el número de abajo (el denominador) se vuelve cero. En el ejemplo, si Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 4x-12=0 , entonces
. Así que, en , esta función tiene una singularidad.
- Otras funciones: La función logaritmo (Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): y(x)=\log x ) tiene una singularidad cuando
es cero o un número negativo. La función tangente (Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): y(x)=\tan x ) también tiene singularidades en ciertos puntos, como 90 grados o 270 grados, donde su valor se vuelve infinito.
Galería de imágenes
-
Una imagen que muestra cómo una función matemática puede comportarse de forma extraña en un punto específico, llamado singularidad.
Véase también
En inglés: Singularity (mathematics) Facts for Kids
- Punto crítico
- Extremos de una función
- Clasificación de discontinuidades
