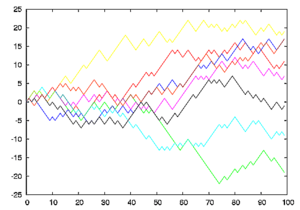
Camino aleatorio para niños
La caminata aleatoria o paseo aleatorio es un concepto matemático que describe el camino que se forma al dar pasos sucesivos al azar. Imagina que estás en un punto y, sin saber a dónde ir, das un paso en cualquier dirección. Luego, desde tu nueva posición, vuelves a dar otro paso al azar, y así sucesivamente. La trayectoria que dibujas es una caminata aleatoria.
Este concepto es muy útil para entender cómo se mueven las cosas en el mundo real. Por ejemplo, el recorrido de una molécula en un líquido o gas, el camino que sigue un animal buscando comida, o incluso cómo cambia el precio de una acción en la bolsa, pueden ser vistos como caminatas aleatorias.
El término "caminata aleatoria" fue introducido por el científico Karl Pearson en 1905. Desde entonces, los estudios sobre las caminatas aleatorias se han aplicado en muchos campos, como la informática, la física, la química, la ecología, la biología, la psicología y la economía.
En economía, por ejemplo, la idea de que los precios de las acciones se mueven de forma aleatoria es una parte importante de la "hipótesis de los mercados eficientes". En física, ayuda a entender el movimiento browniano, que es el movimiento caótico de partículas pequeñas en un fluido. En ecología, se usa para modelar cómo se mueven los animales.
Existen diferentes tipos de caminatas aleatorias. Algunas se estudian en espacios simples como una línea, un plano o espacios con más dimensiones. Otras se dan en estructuras más complejas llamadas "grafos" (como redes de puntos conectados). A menudo, las caminatas aleatorias se consideran un tipo de cadena de Márkov, que son procesos donde el futuro solo depende del estado actual, no de cómo se llegó a él.
En general, una caminata aleatoria es cualquier proceso donde la posición de algo en un momento dado solo depende de su posición anterior y de un factor aleatorio que decide la siguiente dirección y la longitud del paso.
Contenido
¿Qué es una Caminata Aleatoria?
Una caminata aleatoria se puede entender como una secuencia de posiciones donde cada nueva posición se obtiene sumando un paso aleatorio a la posición anterior.
La Propiedad de Márkov
Una característica importante de muchas caminatas aleatorias es la "Propiedad de Márkov". Esto significa que la dirección y la longitud del siguiente paso solo dependen de dónde te encuentras ahora, no de dónde estuviste antes. Es como si el camino "olvidara" su historia y solo le importara su ubicación actual para decidir el siguiente movimiento.
Las caminatas aleatorias pueden ocurrir en cualquier número de dimensiones (una línea, un plano, el espacio tridimensional), pueden ser "parciales" (con una dirección preferida) o "imparciales" (todas las direcciones son igual de probables), y pueden ser "discretas" (pasos en momentos específicos) o "continuas" (movimiento constante).
Caminatas Aleatorias en Grafos
A veces, el espacio donde ocurre una caminata aleatoria se puede representar como un "grafo". Un grafo es un conjunto de puntos (llamados vértices) conectados por líneas (llamadas aristas).
Imagina que estás en un vértice de un grafo y eliges al azar uno de sus vértices vecinos para moverte. Luego, desde ese nuevo vértice, eliges otro vecino al azar, y así sucesivamente. La secuencia de vértices que visitas forma una caminata aleatoria sobre ese grafo.
Las caminatas aleatorias en grafos son muy importantes en matemáticas y física. Por ejemplo, cuando barajas un mazo de cartas, puedes pensar en cada posible orden de las cartas como un vértice en un grafo. Barajar las cartas es como hacer una caminata aleatoria en ese grafo, moviéndote de una permutación a otra.
Los científicos estudian cuánto tiempo se tarda en volver al punto de partida, en llegar a un vértice específico o en visitar todos los vértices del grafo.
Caminata Aleatoria Simétrica
Un tipo común es la "caminata aleatoria simétrica". En este caso, si estás en un vértice, tienes la misma probabilidad de moverte a cualquiera de sus vértices vecinos. Es como si todas las opciones fueran igual de atractivas.
Caminatas Aleatorias en Cuadrículas
Las caminatas aleatorias en cuadrículas, como las que forman las calles de una ciudad (que se pueden representar como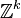 
), son muy interesantes.
Caminata en una Línea (1D)
Imagina que caminas en una línea recta, dando pasos hacia adelante o hacia atrás. Si la probabilidad de ir hacia adelante es la misma que la de ir hacia atrás (por ejemplo, 50% y 50%), se dice que es una caminata simétrica. En este caso, si empiezas en un punto, ¡siempre volverás a ese punto en algún momento!
Esto se relaciona con el "problema de la ruina del apostador": si un jugador con dinero limitado juega contra alguien con dinero ilimitado en un juego justo, el jugador siempre terminará perdiendo todo su dinero. Su dinero hará una caminata aleatoria y, tarde o temprano, llegará a cero.
Caminata en un Plano (2D)
Si caminas en un plano (como un mapa), eligiendo al azar una de las cuatro direcciones (arriba, abajo, izquierda, derecha) en cada cruce, también es una caminata aleatoria. Al igual que en una línea, si empiezas en un punto, ¡siempre volverás a ese punto en algún momento!
Caminata en el Espacio (3D o más)
Pero si la caminata ocurre en tres dimensiones o más, la historia cambia. En este caso, es posible que nunca regreses al punto de partida. Imagina un pájaro despistado volando al azar por el cielo; podría vagar para siempre sin encontrar su nido.
Aplicaciones de las Caminatas Aleatorias
Las caminatas aleatorias tienen muchas aplicaciones prácticas:
- En genética, ayudan a entender cómo cambian las características de una población a lo largo del tiempo.
- En física, son modelos simples para el movimiento browniano (el movimiento aleatorio de moléculas) y la difusión.
- En biología, se usan para describir cómo se mueven los animales y cómo se dispersan las especies.
- En matemáticas, se utilizan para resolver ecuaciones complejas y para estudiar diferentes estructuras.
- En informática, se emplean para estimar el tamaño de la World Wide Web o para procesar imágenes, por ejemplo, para separar un objeto del fondo en una foto.
- En arte, algunas esculturas, como Quantum Cloud de Antony Gormley, han sido diseñadas usando algoritmos de caminatas aleatorias.
Relación con el Movimiento Browniano
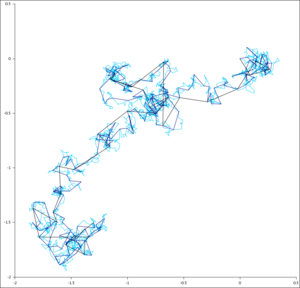
El movimiento browniano es el movimiento aleatorio de partículas muy pequeñas en un fluido. Las caminatas aleatorias son como una versión "paso a paso" de este movimiento.
Si los pasos en una caminata aleatoria se hacen cada vez más pequeños y el número de pasos aumenta, la caminata se parece cada vez más a un proceso de Wiener, que es un modelo matemático del movimiento browniano.
Una caminata aleatoria es un tipo de fractal discreto. Un fractal es una forma geométrica que se repite a diferentes escalas. La trayectoria de un proceso de Wiener es un fractal "auténtico". Por ejemplo, en dos dimensiones, el camino de un proceso de Wiener tiene una "dimensión fractal" de 2, lo que significa que es tan complejo que casi llena el plano.
Véase también
En inglés: Random walk Facts for Kids
