Cadena de Márkov para niños

Una cadena de Márkov es un concepto matemático que nos ayuda a entender cómo cambian las cosas con el tiempo. Imagina una secuencia de eventos, como el clima día a día. Lo especial de una cadena de Márkov es que la probabilidad de lo que ocurra a continuación depende solamente de lo que está pasando justo ahora, no de todo lo que ha pasado antes.

Esta característica se llama la propiedad de Márkov. Es como si el sistema solo tuviera "memoria" del último paso. Por ejemplo, si hoy llueve, la probabilidad de que mañana llueva o haga sol solo depende de que hoy esté lloviendo, no de si llovió la semana pasada.

El matemático ruso Andréi Márkov (1856-1922) fue quien introdujo esta idea en 1906. Él definió una "cadena simple" como una serie de eventos donde cada evento futuro solo depende del evento actual.

Las cadenas de Márkov son muy útiles y se usan en muchas áreas para predecir o entender patrones.

Una cadena simple de Márkov con dos estados posibles.

¿Qué es una Cadena de Márkov?

Una cadena de Márkov es un tipo de proceso estocástico (un proceso que cambia de forma aleatoria con el tiempo) donde el futuro solo depende del presente. No importa cómo llegamos al estado actual; lo único que importa es dónde estamos ahora.

Estados y Transiciones

En una cadena de Márkov, los "estados" son las diferentes situaciones en las que puede estar el sistema. Por ejemplo, si hablamos del clima, los estados podrían ser "soleado", "nublado" o "lluvioso".

Las "transiciones" son los cambios de un estado a otro. Cada transición tiene una "probabilidad de transición", que es la posibilidad de pasar de un estado a otro en un solo paso de tiempo. Por ejemplo, la probabilidad de pasar de "soleado" a "lluvioso".

Cadenas Homogéneas

Una cadena de Márkov es "homogénea" si las probabilidades de transición no cambian con el tiempo. Esto significa que la probabilidad de ir del estado A al estado B es la misma hoy, mañana o en cualquier momento. Si estas probabilidades cambian, la cadena es "no homogénea".

Matriz de Probabilidades de Transición

Podemos organizar todas las probabilidades de transición en una tabla especial llamada "matriz de probabilidades de transición". Esta matriz nos muestra la probabilidad de pasar de cualquier estado a cualquier otro estado en un solo paso.

Por ejemplo, si tenemos los estados 0, 1 y 2, la matriz se vería así: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): P= \begin{bmatrix} p_{00} & p_{01} & p_{02} \\ p_{10} & p_{11} & p_{12} \\ p_{20} & p_{21} & p_{22} \end{bmatrix} Donde 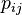es la probabilidad de ir del estado al estado 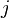. Cada fila de esta matriz suma 1, porque desde un estado siempre tenemos que ir a algún otro estado (o quedarnos en el mismo).

Clases de Comunicación

En una cadena de Márkov, decimos que un estado se "comunica" con otro si podemos ir de uno al otro y viceversa. Si todos los estados de una cadena se comunican entre sí, decimos que la cadena es "irreducible". Esto significa que, sin importar dónde empecemos, podemos llegar a cualquier otro estado.

Periodicidad

Algunos estados en una cadena de Márkov pueden tener un "periodo". Esto significa que solo podemos volver a ese estado después de un número específico de pasos (o múltiplos de ese número). Si un estado no tiene un periodo fijo (es decir, podemos volver en cualquier número de pasos), se le llama "aperiódico". Una cadena es aperiódica si todos sus estados lo son.

Recurrencia y Transitoriedad

• Un estado es "recurrente" si, una vez que llegamos a él, es seguro que volveremos a visitarlo en el futuro.
• Un estado es "transitorio" si, una vez que lo abandonamos, hay una posibilidad de que nunca volvamos a él.

Si una cadena es irreducible y todos sus estados son recurrentes, se dice que es "recurrente positiva".

Distribuciones Estacionarias

Imagina que una cadena de Márkov ha estado funcionando por mucho tiempo. Si las probabilidades de estar en cada estado se estabilizan y ya no cambian, decimos que ha alcanzado una "distribución estacionaria". Es como un equilibrio donde la proporción de tiempo que pasamos en cada estado se mantiene constante.

Si una cadena de Márkov es irreducible, aperiódica y recurrente positiva, entonces siempre tendrá una única distribución estacionaria. Además, con el tiempo, la probabilidad de estar en cualquier estado se acercará a los valores de esta distribución estacionaria.

Tipos de Cadenas de Márkov

Cadenas Irreducibles

Como mencionamos, una cadena de Márkov es irreducible si desde cualquier estado se puede llegar a cualquier otro estado. Esto significa que todos los estados están conectados.

Cadenas Absorbentes

Una cadena de Márkov es "absorbente" si tiene al menos un estado al que, una vez que se llega, no se puede salir. Estos se llaman "estados absorbentes". Además, desde cualquier estado que no sea absorbente, siempre se puede llegar a un estado absorbente. Esto significa que, tarde o temprano, la cadena terminará en uno de esos estados.

Aplicaciones de las Cadenas de Márkov

Las cadenas de Márkov son herramientas muy poderosas y se usan en muchos campos:

• Meteorología: Para crear modelos básicos del clima y predecir patrones de lluvia, asumiendo que el clima de mañana solo depende del de hoy.
• Modelos de Propagación: Se usan para entender cómo se propagan ciertas cosas, como ideas o incluso enfermedades, en una población.
• Internet: El famoso algoritmo PageRank de Google, que ayuda a clasificar las páginas web en los resultados de búsqueda, se basa en una cadena de Márkov. Imagina que un usuario navega por la web haciendo clics aleatorios; la cadena modela la probabilidad de que el usuario termine en una página específica.
• Simulación: Ayudan a resolver problemas en áreas como la gestión de filas (teoría de colas), por ejemplo, para saber cuánto tiempo esperará la gente en una fila.
• Juegos de Azar: Se pueden usar para analizar juegos de azar, como la probabilidad de que un jugador pierda todo su dinero en un juego.
• Economía y Finanzas: Para analizar patrones de compra, planificar necesidades de personal o estudiar el comportamiento de los mercados.
• Genética: En la genética de poblaciones, se usan para describir cómo cambian las frecuencias de los genes en una población a lo largo de las generaciones.
• Música: Algunos programas y compositores usan cadenas de Márkov para crear música, generando secuencias de notas o acordes basadas en probabilidades.
• Operaciones: Se aplican en la gestión de inventarios, el mantenimiento de equipos y el análisis del flujo de procesos en empresas.
• Inteligencia Artificial: Se utilizan en algunas redes neuronales, como las máquinas de Boltzmann.

Véase también

En inglés: Markov chain Facts for Kids