Paralelismo (matemática) para niños
En geometría, el paralelismo es una relación especial que existe entre líneas, planos o figuras similares que nunca se encuentran, por mucho que se extiendan. Imagina las vías de un tren: siempre van una al lado de la otra y nunca se cruzan. Eso es el paralelismo.
En un plano cartesiano (como una cuadrícula), dos rectas son paralelas si tienen la misma inclinación (llamada pendiente). Si una recta sube o baja de la misma manera que otra, entonces son paralelas.
También, una recta y un plano pueden ser paralelos, o dos planos entre sí. Esto significa que no tienen ningún punto en común.
Contenido
¿Qué es el Paralelismo en Geometría?
El paralelismo es una idea fundamental en la geometría. Se aplica a diferentes tipos de figuras que se extienden en una dirección, como las rectas o los planos.
Paralelismo en el Plano: Rectas que Nunca se Tocan
Cuando hablamos de dos rectas en un mismo plano, decimos que son paralelas si:
- Son la misma recta (están una encima de la otra).
- O, lo más común, nunca se cruzan, por mucho que las alarguemos.
¿Cómo saber si dos rectas son paralelas?
En la geometría euclidiana (la que estudiamos normalmente), si tenemos dos rectas, l y m, en un plano, podemos saber si son paralelas por estas características:
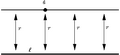
- Distancia constante: Todos los puntos de la recta m están a la misma distancia de la recta l. Es como si siempre mantuvieran la misma separación.
- Nunca se intersecan: Las rectas m y l están en el mismo plano, pero no se tocan en ningún punto. Esta es la definición más usada.
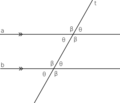
- Ángulos iguales con una transversal: Si una tercera recta (llamada transversal) corta a las dos rectas paralelas, los ángulos que se forman en las intersecciones son iguales. Por ejemplo, los ángulos correspondientes (los que están en la misma posición en cada cruce) son idénticos.
La segunda característica (que nunca se intersecan) es la más sencilla y se usa como la definición principal de rectas paralelas en la geometría euclidiana. Las otras características son consecuencias de esta idea.
Paralelismo en el Espacio: Planos y Rectas
El concepto de paralelismo también se aplica a figuras en el espacio tridimensional.
Planos paralelos
En el espacio, dos planos son paralelos si:
- Son el mismo plano.
- O, no tienen ninguna recta en común, es decir, nunca se cruzan. Imagina el suelo y el techo de una habitación: son planos paralelos.
Rectas y planos paralelos
Una recta y un plano también pueden ser paralelos. Esto ocurre si la recta no está dentro del plano y nunca lo cruza.
Rectas paralelas en el espacio
Dos rectas en el espacio tridimensional son paralelas si están en un mismo plano y no se cruzan. Si no están en el mismo plano y no se cruzan, se les llama "rectas oblicuas".
El Símbolo del Paralelismo
Para indicar que dos líneas o figuras son paralelas, usamos un símbolo especial: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \parallel . Por ejemplo, si escribimos Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): AB \parallel CD , significa que la línea AB es paralela a la línea CD.
Propiedades Importantes de las Rectas Paralelas
Las rectas paralelas tienen algunas propiedades muy interesantes que las hacen especiales en geometría.
El Axioma de Unicidad de Euclides
Un axioma es una verdad que se acepta sin necesidad de demostración. En la geometría euclidiana, hay un axioma muy importante sobre las rectas paralelas:
- En un plano, si tienes una recta y un punto fuera de ella, solo puedes dibujar una única recta que pase por ese punto y sea paralela a la primera recta.
Relación de Paralelismo: ¿Qué significa?
El paralelismo es una relación binaria entre rectas. Esto significa que podemos decir si dos rectas están relacionadas por el paralelismo. Si tenemos tres rectas (a, b, c) en un plano, se cumplen estas propiedades:
- Reflexiva: Toda recta es paralela a sí misma. (a Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \parallel a)
- Simétrica: Si una recta es paralela a otra, entonces la segunda también es paralela a la primera. Si a Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \parallel b, entonces b Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \parallel a.
- Transitiva: Si una recta es paralela a una segunda, y esta segunda es paralela a una tercera, entonces la primera es paralela a la tercera. Si a Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \parallel b y b Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \parallel c, entonces a Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \parallel c.
Gracias a estas propiedades, decimos que el paralelismo es una relación de equivalencia. Estas mismas propiedades se aplican a los planos paralelos en el espacio.
Teoremas Clave sobre Rectas Paralelas
Un teorema es una afirmación que se puede demostrar. Aquí hay dos teoremas importantes sobre las rectas paralelas:
- En un plano, si dos rectas son perpendiculares (forman un ángulo de 90 grados) a una tercera recta, entonces esas dos rectas son paralelas entre sí.
- Si en un plano una recta corta a otra, entonces también cortará a todas las rectas que sean paralelas a esta última.
¿Cómo construir líneas paralelas?
Existen diferentes métodos para dibujar una línea paralela a otra, pasando por un punto dado, usando solo una regla y un compás. Estos métodos se basan en las propiedades que hemos visto.
¿Cómo se mide la distancia entre líneas paralelas?
Como las rectas paralelas en un plano siempre están a la misma distancia, podemos calcular esa distancia. Si tenemos las ecuaciones de dos rectas paralelas, podemos usar fórmulas para encontrar la distancia más corta entre ellas. Por ejemplo, si las rectas son Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): y = mx+b_1 y Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): y = mx+b_2 , la distancia entre ellas es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): d = \frac{|b_2-b_1|}{\sqrt{m^2+1}} .
Paralelismo en otras Geometrías
La geometría euclidiana es la que aprendemos primero, pero existen otras geometrías llamadas "no euclidianas". En ellas, el concepto de paralelismo puede ser un poco diferente. En estas geometrías, en lugar de "líneas", a menudo hablamos de "geodésicas", que son los caminos más cortos entre dos puntos.
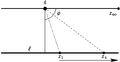
Geometría Hiperbólica
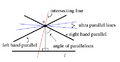
En la geometría hiperbólica, si tienes una geodésica (línea) y un punto fuera de ella, ¡pueden pasar infinitas geodésicas por ese punto que no se cruzan con la primera! Algunas de estas se llaman "paralelas" (porque se acercan mucho en el infinito) y otras "ultra paralelas" (porque se alejan entre sí).
Geometría Esférica
En la geometría esférica (como la superficie de una esfera), todas las geodésicas son "grandes círculos" (como el ecuador en un globo terráqueo). Todos los grandes círculos se cruzan entre sí. Por lo tanto, en una esfera, ¡no existen las geodésicas paralelas! Todas se encuentran en algún punto. Las "líneas" que son equidistantes en una esfera se llaman "paralelos de latitud", como los círculos de latitud en un mapa.
Galería de imágenes
-
Error al crear miniatura: convert: no images defined `/var/www/spanish/tmp/transform_f3a7a3f5f137.png' @ error/convert.c/ConvertImageCommand/3229.
Error code: 1En la esfera, no existen las líneas paralelas. Todas las geodésicas se cruzan.
Véase también
 En inglés: Parallel (geometry) Facts for Kids
En inglés: Parallel (geometry) Facts for Kids