Orden de magnitud para niños
El orden de magnitud de un número nos ayuda a entender qué tan grande o pequeño es algo, comparándolo con potencias de diez. Imagina que quieres comparar el tamaño de una hormiga con el de un elefante. En lugar de usar números muy largos o muy pequeños, el orden de magnitud nos da una idea rápida de la diferencia.
Se dice que dos números tienen un orden de magnitud diferente si uno es aproximadamente diez veces más grande o más pequeño que el otro. Por ejemplo, si un número es 100 veces más grande que otro, decimos que difieren en 2 órdenes de magnitud (porque 100 es 10 x 10, o 102).
Para expresar el orden de magnitud, usamos la notación científica, que se basa en potencias de diez. Por ejemplo, el número 1500 se puede escribir como 1.5 × 103. Su orden de magnitud es 3, porque el 10 está elevado a la potencia de 3.
Contenido
¿Para qué usamos los órdenes de magnitud?
Los órdenes de magnitud son muy útiles para comparar de forma sencilla el tamaño de objetos o distancias en el Universo. Nos permiten tener una idea rápida de las diferencias entre cosas muy grandes y muy pequeñas.
Comparando tamaños de forma sencilla
Si un número "A" es aproximadamente diez veces más grande que un número "B", decimos que "A" difiere en un orden de magnitud de "B". Si "A" es unas 100 veces más grande que "B", entonces difiere en dos órdenes de magnitud.
Dos números tienen el mismo orden de magnitud si el más grande de ellos es menos de diez veces mayor que el otro. Esto significa que están en una escala similar.
¿Cómo se representan los órdenes de magnitud?
Los órdenes de magnitud se representan usando potencias de base 10. Esto significa que los escribimos como "10n" o simplemente como "n". La "n" es un número entero que puede ser positivo (para números grandes) o negativo (para números pequeños).
Por ejemplo, un kilogramo (1000 gramos) tiene un orden de magnitud de "diez elevado a tres" (103) o simplemente un orden de magnitud "tres".
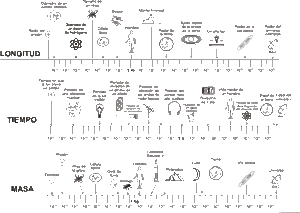
Ejemplos de órdenes de magnitud en el universo
La gran ventaja de los órdenes de magnitud es que nos ayudan a entender el tamaño relativo de las cosas, desde lo más diminuto hasta lo más inmenso.
- Una célula (en metros) tiene un orden de magnitud de 10-5 metros.
- Una fruta (como una manzana) tiene un orden de magnitud de 10-1 metros (o 10 centímetros).
- Los planetas tienen un orden de magnitud de 107 metros (o 10 millones de kilómetros).
- Las galaxias tienen un orden de magnitud de 1021 metros.
Para comparar estos tamaños, solo necesitamos restar los exponentes:
- Una galaxia es 14 órdenes de magnitud mayor que un planeta (21 - 7 = 14).
- Un planeta es 8 órdenes de magnitud mayor que una fruta (7 - (-1) = 8).
- Una fruta es 4 órdenes de magnitud mayor que una célula (-1 - (-5) = 4).
Galería de imágenes
-
Escenas y objetos ejemplo de diferente orden de magnitud. Desde la espuma cuántica (10-32 m) hasta el universo observable (1026 m).
.png){kind=small}
Véase también
En inglés: Order of magnitude Facts for Kids
- Anexo:Orden de magnitud
- Órdenes de magnitud (longitud)
- Órdenes de magnitud (superficie)
- Órdenes de magnitud (volumen)
- Órdenes de magnitud (energía)
