Conectiva lógica para niños

Enciclopedia para niños

Una conectiva lógica es como una palabra o un símbolo especial que se usa para unir dos frases o ideas. Cuando las unimos, el valor de verdad de la frase nueva (es decir, si es verdadera o falsa) depende de si las frases originales eran verdaderas o falsas.

Las conectivas lógicas más comunes unen dos frases, como si fueran los "ingredientes" de una nueva idea. La negación, que significa "no", es una conectiva que se aplica a una sola frase.

Estas conectivas son muy importantes en la lógica, que es el estudio del razonamiento, y también en la programación de computadoras. Nos ayudan a combinar ideas y a entender cómo se relacionan entre sí.

Conectivas Lógicas: Cómo Unen Ideas

Las conectivas lógicas son herramientas que nos permiten construir frases más complejas a partir de frases más sencillas. Piensa en ellas como el "pegamento" que une las ideas. Lo interesante es que, al unirlas, podemos saber si la nueva frase es verdadera o falsa, solo conociendo la verdad de las frases que la forman.

Conectivas en el Lenguaje Diario

En nuestro día a día, usamos palabras para unir frases. Por ejemplo, si tenemos estas dos ideas:

Juan subió la montaña.
Eduardo subió la montaña.

Podemos unirlas con la palabra "y" para formar:

Juan subió la montaña y Eduardo subió la montaña.

Aquí, la palabra "y" actúa como una conectiva lógica. Si Juan subió la montaña es verdad Y Eduardo subió la montaña es verdad, entonces la frase completa con "y" también es verdad. Si una de las dos no es verdad, la frase completa con "y" es falsa.

También podemos usar "por lo tanto":

Juan subió la montaña, por lo tanto Eduardo subió la montaña.

Esta frase también usa una conectiva lógica, porque la verdad de la segunda parte depende de la primera.

Conectivas en Lenguajes de Computación y Lógica

En campos como la lógica y la programación, usamos símbolos especiales para estas conectivas. Esto ayuda a que no haya confusiones, ya que cada símbolo tiene un significado exacto. A estos símbolos se les llama "conectivos lógicos" u "operadores lógicos".

Los conectivos lógicos pueden unir más de dos ideas a la vez, aunque lo más común es que unan dos.

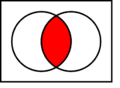
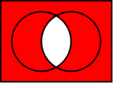
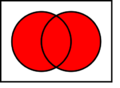
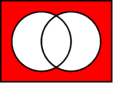
Conectiva	Símbolo	Ejemplo de uso	En el lenguaje diario	Ejemplo en lenguaje diario	Tabla de verdad
Negación	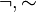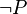$\neg,\sim \,$	$\neg P \,$	no	No está lloviendo.	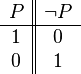$\begin{array}{c\|\|c} P & \neg P \\ \hline 1 & 0 \\ 0 & 1 \\ \end{array}$
Conjunción	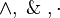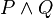$\land,\And, \cdot \,$	$P \land Q \,$	y	Está lloviendo y la calle está mojada.	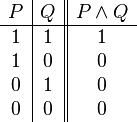$\begin{array}{c\|c\|\|c} P & Q & P \land Q \\ \hline 1 & 1 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \\ \end{array}$
Disyunción	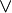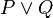$\lor \,$	$P \lor Q \,$	o	Está lloviendo o la calle está mojada.	$\begin{array}{c\|c\|\|c} P & Q & P \lor Q \\ \hline 1 & 1 & 1 \\ 1 & 0 & 1 \\ 0 & 1 & 1 \\ 0 & 0 & 0 \\ \end{array}$
Condicional material	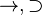$\to,\supset$	$P \to Q \,$	si... entonces	Si está lloviendo, entonces la calle está mojada.	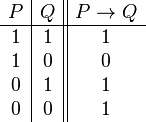$\begin{array}{c\|c\|\|c} P & Q & P \to Q \\ \hline 1 & 1 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 1 \\ 0 & 0 & 1 \\ \end{array}$
Bicondicional	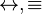$\leftrightarrow, \equiv \,$	$P \leftrightarrow Q \,$	si y solo si	Está lloviendo si y solo si la calle está mojada.	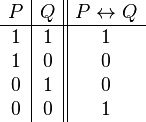$\begin{array}{c\|c\|\|c} P & Q & P \leftrightarrow Q \\ \hline 1 & 1 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{array}$
Negación conjunta	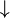$\downarrow \,$	$P \downarrow Q \,$	ni... ni	Ni está lloviendo ni la calle está mojada.	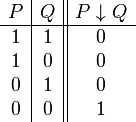$\begin{array}{c\|c\|\|c} P & Q & P \downarrow Q \\ \hline 1 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{array}$
Disyunción excluyente	$\nleftrightarrow, \oplus, \not\equiv, W , \underline{\vee}$	$P \nleftrightarrow Q \,$	o bien... o bien	O bien está lloviendo, o bien la calle está mojada.	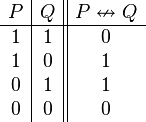$\begin{array}{c\|c\|\|c} P & Q & P \nleftrightarrow Q \\ \hline 1 & 1 & 0 \\ 1 & 0 & 1 \\ 0 & 1 & 1 \\ 0 & 0 & 0 \\ \end{array}$

Tipos Comunes de Conectivas Lógicas

Aquí te mostramos las conectivas lógicas más usadas y cómo funcionan:

Negación (NO): Se usa para decir lo contrario de una idea. Si "Está lloviendo" es verdad, "NO está lloviendo" es falso.

* Símbolos: ¬, ~

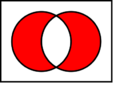
Conjunción (Y): Une dos ideas y la frase completa es verdad solo si AMBAS ideas son verdaderas.

* Símbolos: ∧, y, ∙ * Ejemplo: "Está lloviendo y estoy dentro de casa." Esto es verdad solo si las dos cosas pasan al mismo tiempo.

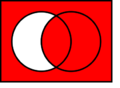
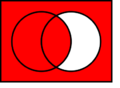
Disyunción (O): Une dos ideas y la frase completa es verdad si AL MENOS UNA de las ideas es verdadera.

* Símbolo: ∨ * Hay dos tipos de "o": * Inclusivo: La frase es verdad si una, la otra, o ambas ideas son verdaderas. Ejemplo: "Está lloviendo o estoy dentro de casa." Esto es verdad si llueve, si estoy dentro, o si ambas cosas pasan. * Exclusivo (XOR): La frase es verdad si una idea es verdadera, O la otra es verdadera, pero NO AMBAS al mismo tiempo. Ejemplo: "O bien voy al cine, o bien voy al parque." No puedes hacer las dos cosas a la vez.

Condicional (Si... entonces): Indica que si la primera idea es verdadera, la segunda también debe serlo.

* Símbolos: →, ⇒, ⊃ * Ejemplo: "Si está lloviendo, entonces estoy en casa." Si llueve y no estoy en casa, la frase es falsa.

Bicondicional (si y solo si): Significa que las dos ideas son verdaderas o falsas al mismo tiempo. Una depende completamente de la otra.

* Símbolos: ↔, ≡, = * Ejemplo: "Estoy dentro si y solo si está lloviendo." Esto significa que estoy dentro si llueve, y si no llueve, no estoy dentro.

También existen ideas que siempre son verdaderas (llamadas Verdad o Tautología) y las que siempre son falsas (llamadas Falso o Contradicción).

Relaciones entre Conectivas

Algunas conectivas tienen relaciones especiales. Por ejemplo, la frase "Si P entonces Q" (P→Q) es equivalente a "Si no Q entonces no P" (¬Q→¬P). Esto significa que ambas frases siempre tienen el mismo valor de verdad.

Por ejemplo, si tenemos la frase: "Si viene Juan, no iré de acampada."

Su equivalente sería: "Si voy de acampada, entonces no viene Juan."

Historia de los Símbolos

Los símbolos que usamos para las conectivas lógicas han cambiado a lo largo del tiempo. Por ejemplo:

El símbolo de negación (¬) apareció en 1929. Antes se usaban otros.
El símbolo de conjunción (∧) también apareció en 1929.
El símbolo de disyunción (∨) fue usado por primera vez en 1908.
Para la implicación (→), se empezó a usar en 1917.
El bicondicional (↔) se usó desde 1940.

Muchos lógicos y matemáticos famosos como Gottlob Frege, Bertrand Russell y George Boole contribuyeron a desarrollar estos símbolos y la forma en que entendemos la lógica.

Conectivas en la Computación

En el mundo de las computadoras, las conectivas lógicas son fundamentales. Se usan para construir los circuitos digitales que hacen funcionar todos los aparatos electrónicos. Las puertas lógicas son componentes electrónicos que implementan estas conectivas (como AND, OR, NOT) y son la base de cómo las computadoras procesan la información.

Por ejemplo, cuando un programa de computadora dice "si (condición P) entonces (acción Q)", está usando una lógica similar a la conectiva "si... entonces". Si la condición P es verdadera, la acción Q se ejecuta. Si P es falsa, Q no se ejecuta.

Conectivas según sus Argumentos

Podemos clasificar las conectivas según cuántas ideas o "argumentos" necesitan para funcionar:

Sin Argumentos

Son ideas que siempre son verdaderas o siempre son falsas, sin depender de nada más.

Verdad ( $\top$ ): Siempre es verdadera.
Falso ( $\bot$ ): Siempre es falsa.

Con un Argumento

Solo necesitan una idea para funcionar.

Afirmación ( 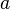$a \,$ ): Simplemente la idea original.
Negación ( 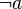$\neg a$ ): Lo contrario de la idea original.

Con dos Argumentos

Necesitan dos ideas para unirlas.

Disyunción ( 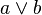$a\lor b$ ): "a o b"
Conjunción ( 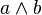$a\land b$ ): "a y b"
Implicación ( $a\to b$ ): "Si a entonces b"
Bicondicional ( $a\leftrightarrow b$ ): "a si y solo si b"

Galería de imágenes

Verdad
Falso
Proposición P
Negación
Conjunción
Conjunción Opuesta
Disyunción
Disyunción Opuesta
Condicional
O exclusivo
Bicondicional
Implicación Opuesta
Proposición P
Proposición Q
Símbolo de negación de Frege

Véase también

En inglés: Logical connective Facts for Kids

Función booleana
Lógica booleana
Constante lógica

Cálculo proposicional
Función de verdad
Tabla de verdad
Valor de verdad

Obtenido de «https://ninos.kiddle.co/index.php?title=Conectiva_lógica&oldid=4884936»

Todo el contenido de los artículos de la Enciclopedia Kiddle (incluidas las imágenes) se puede utilizar libremente para fines personales y educativos bajo la licencia Atribución-CompartirIgual a menos que se indique lo contrario. Citar este artículo:

Conectiva lógica para Niños. Enciclopedia Kiddle.