Notación flecha de Knuth para niños
La notación flecha de Knuth es una forma especial de escribir números que son increíblemente grandes. Fue creada por un matemático llamado Donald Knuth en 1976. Esta notación nos ayuda a entender y trabajar con números tan enormes que no cabrían en una calculadora normal.
La idea principal es que podemos pensar en las operaciones matemáticas como pasos que se repiten. Por ejemplo:
- La multiplicación es como una suma que se repite.
* Por ejemplo, 4 × 3 significa sumar 4 tres veces: 4 + 4 + 4 = 12.
- La potenciación (cuando elevas un número a una potencia, como 4 elevado a 3, que se escribe 4³) es como una multiplicación que se repite.
* Knuth usa una flecha hacia arriba para esto: 
es lo mismo que 
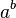. * Por ejemplo, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 4 \uparrow 3 significa multiplicar 4 tres veces: 4 × 4 × 4 = 64.
Contenido
¿Cómo funciona la notación flecha de Knuth?
La flecha doble (↑↑)
Para hacer números aún más grandes, Knuth inventó la "doble flecha" (
). Esta significa que la operación de potenciación se repite. A esto se le llama tetración.
significa que elevas 'a' a la potencia de 'a', y así sucesivamente, 'b' veces. Es como una "torre de potencias".- Se calcula de derecha a izquierda.
Por ejemplo:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 4 \uparrow\uparrow 3 significa
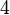elevado a ( 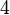elevado a ).
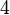* Primero calculamos Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 4 \uparrow 4 (que es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 4^4 = 256 ). * Luego, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 4 \uparrow 256 (que es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 4^{256} ). * Este número es gigantesco, ¡aproximadamente 1.34 seguido de 154 ceros!
Veamos otro ejemplo con números más pequeños:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 3 \uparrow\uparrow 2 = 3^3 = 27 .
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 3 \uparrow\uparrow 3 = 3^{3^3} = 3^{27} = 7,625,597,484,987 . ¡Ya es un número enorme!
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 3 \uparrow\uparrow 4 = 3^{3^{3^3}} = 3^{3^{27}} . Este número es tan grande que tiene más de 3 billones de dígitos.
Más flechas: triple, cuádruple y más
Knuth no se detuvo ahí. También definió la "triple flecha" (Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \uparrow\uparrow\uparrow ) para la pentación, que es la tetración repetida. Y luego la "cuádruple flecha" (Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \uparrow\uparrow\uparrow\uparrow ) para la hexación, y así sucesivamente.
La regla es sencilla:
- Un operador con
flechas significa que repites la operación con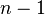 
flechas. - Por ejemplo,
significa que repites la operación Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a \uparrow\uparrow 'b' veces.
Un ejemplo con la triple flecha:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 3 \uparrow\uparrow\uparrow 2 = 3 \uparrow\uparrow 3 .
* Como vimos antes, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 3 \uparrow\uparrow 3 = 3^{3^3} = 3^{27} = 7,625,597,484,987 .
Para hacer la escritura más corta, a veces se usa 
para representar 
con flechas y 
. Por ejemplo, 
es lo mismo que 
.
¿Por qué se usa esta notación?
Normalmente, cuando escribimos 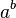, el exponente va arriba de . Pero en computadoras o en mensajes de texto simples, es difícil escribir números así. Por eso, se usa o Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a ^ b .
La notación de Knuth con flechas es muy útil porque nos permite escribir de forma clara y sencilla números que son tan grandes que no podríamos representarlos de ninguna otra manera. Imagina intentar escribir una torre de potencias con cientos o miles de números; ¡sería imposible! La notación flecha lo simplifica.
¿Cómo se ven las torres de potencias?
Cuando escribimos usando la notación de potencias normal, se ve como una torre:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a \uparrow\uparrow 4 es elevado a elevado a elevado a (Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a^{a^{a^a}} ).
Si el número es muy grande, la torre de potencias se vería así: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a \uparrow\uparrow b = a^{a^{(...^a)}} (donde 'a' aparece 'b' veces).
Para , la cosa se vuelve aún más compleja, ¡sería una pila de torres de potencias! Cada torre indicaría la altura de la torre que está encima de ella.
Esta notación es una herramienta poderosa para los matemáticos que trabajan con números extremadamente grandes en campos como la teoría de números o la informática.
Véase también
En inglés: Knuth's up-arrow notation Facts for Kids
