NP-hard para niños
En el mundo de la complejidad computacional, que estudia qué tan difíciles son los problemas para las computadoras, existe una categoría llamada NP-hard (a veces también "NP-difícil"). Esta categoría agrupa problemas que son, al menos, tan complicados de resolver como los problemas más difíciles de la clase NP.
Imagina que tienes una colección de rompecabezas. La clase NP-hard contiene los rompecabezas más difíciles de todos. Si pudieras encontrar una forma muy rápida de resolver uno de estos rompecabezas NP-hard, entonces automáticamente tendrías una forma rápida de resolver cualquier otro rompecabezas de la clase NP. Esto se debe a que cualquier problema de NP se puede "transformar" en un problema NP-hard de manera sencilla.
Contenido
¿Qué significa NP-hard?
La clase NP-hard incluye problemas de decisión, que son aquellos que tienen una respuesta de "sí" o "no". Un problema se considera NP-hard si cualquier otro problema de la clase NP puede convertirse en él usando una "transformación polinómica". Esto significa que la transformación no añade mucha dificultad extra.
Relación con NP-completo
Los problemas NP-completo son un tipo especial de problemas NP-hard. Para que un problema sea NP-completo, debe cumplir dos cosas:
- Debe pertenecer a la clase NP.
- Debe ser tan difícil como cualquier otro problema en NP (es decir, ser NP-hard).
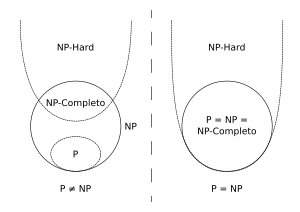
Así que, los problemas NP-completo son la "intersección" entre los problemas NP y los problemas NP-hard. Son los más difíciles dentro de NP.
¿Por qué son importantes los problemas NP-hard?
Si alguien descubriera un método rápido (un algoritmo que funcione en "tiempo polinómico") para resolver un solo problema NP-hard, esto tendría un impacto enorme. Significaría que todos los problemas de la clase NP también podrían resolverse rápidamente. Esto es parte de una de las preguntas más grandes y sin respuesta en la informática: ¿Es P igual a NP? (¿Pueden los problemas que se pueden verificar rápidamente también resolverse rápidamente?).
Un error común es pensar que "NP" en NP-hard significa "no polinómico" (que no se puede resolver rápido). Sin embargo, "NP" viene de "tiempo polinómico no determinista". Aunque se sospecha que no hay algoritmos rápidos para estos problemas, ¡aún no se ha demostrado!
Ejemplos de problemas NP-hard
Para entender mejor, veamos algunos ejemplos de problemas que entran en esta categoría.
El problema de la suma de subconjuntos
Este es un ejemplo de un problema NP-hard. Imagina que tienes un grupo de números, por ejemplo, { -2, 1, 3, -4, 5 }. La pregunta es: ¿Existe algún subconjunto de estos números (sin repetir) que sume exactamente cero? En este caso, sí: { -2, -4, 1, 5 } suma cero. Para conjuntos pequeños es fácil, pero para conjuntos muy grandes, encontrar la respuesta puede ser extremadamente difícil para una computadora.
El problema de parada
Otro ejemplo interesante es el "problema de parada". Este problema consiste en tomar un programa de computadora y sus datos, y decidir si ese programa terminará de ejecutarse o si seguirá funcionando para siempre (en un "bucle infinito").
El problema de parada es NP-hard, pero no es NP-completo. ¿Por qué? Porque es un problema tan difícil que ni siquiera se puede garantizar que una computadora pueda decidirlo siempre. Se le llama un "problema indecidible". Esto significa que no existe un algoritmo general que pueda decirnos con certeza si cualquier programa se detendrá o no. Como los problemas NP-completos deben tener un algoritmo asociado (aunque sea lento), el problema de parada no puede ser NP-completo.
Nombres de las clases de problemas con "NP"
Los nombres de las clases de problemas que incluyen "NP" pueden ser un poco confusos al principio, pero tienen su lógica:
- NP-completo: Son los problemas que son "completos" dentro de la clase NP, es decir, los más difíciles de resolver en NP.
- NP-hard (NP-difícil): Significa que un problema es "al menos" tan difícil como cualquier problema en NP. No necesariamente tiene que estar en NP.
- NP-easy (NP-fácil): Significa que un problema es "como mucho" tan difícil como los problemas en NP.
- NP-equivalente: Significa que un problema es igual de difícil que los problemas en NP.
Véase también
 En inglés: NP-hardness Facts for Kids
En inglés: NP-hardness Facts for Kids
- P (clase de complejidad)
- NP (clase de complejidad)
- NP-completo